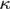 $\kappa$-REALS
$\kappa$-REALSPublished online by Cambridge University Press: 02 July 2019
We investigate some versions of amoeba for tree-forcings in the generalized Cantor and Baire spaces. This answers [10, Question 3.20] and generalizes a line of research that in the standard case has been studied in [11], [13], and [7]. Moreover, we also answer questions posed in [3] by Friedman, Khomskii, and Kulikov, about the relationships between regularity properties at uncountable cardinals. We show 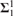 ${\bf{\Sigma }}_1^1$-counterexamples to some regularity properties related to trees without club splitting. In particular we prove a strong relationship between the Ramsey and the Baire properties, in slight contrast with the standard case.
${\bf{\Sigma }}_1^1$-counterexamples to some regularity properties related to trees without club splitting. In particular we prove a strong relationship between the Ramsey and the Baire properties, in slight contrast with the standard case.