No CrossRef data available.
Article contents
U-Lusin sets in hyperfinite time lines
Published online by Cambridge University Press: 12 March 2014
Abstract
In an ω-saturated nonstandard universe a cut is an initial segment of the hyperintegers which is closed under addition. Keisler and Leth in [KL] introduced, for each given cut U, a corresponding U-topology on the hyperintegers by letting O be U-open if for any x ϵ O there is a y greater than all the elements in U such that the interval [x − y,x + y] ⊆ O. Let U be a cut in a hyperfinite time line 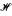 , which is a hyperfinite initial segment of the hyperintegers. A subset B of
, which is a hyperfinite initial segment of the hyperintegers. A subset B of 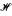 is called a U-Lusin set in
is called a U-Lusin set in 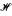 if B is uncountable and for any Loeb-Borel U-meager subset X of
if B is uncountable and for any Loeb-Borel U-meager subset X of 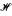 , B ⋂ X is countable. Here a Loeb-Borel set is an element of the σ-algebra generated by all internal subsets of
, B ⋂ X is countable. Here a Loeb-Borel set is an element of the σ-algebra generated by all internal subsets of 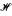 : In this paper we answer some questions of Keisler and Leth about the existence of U-Lusin sets by proving the following facts. (1) If U = x/N = {y ϵ
: In this paper we answer some questions of Keisler and Leth about the existence of U-Lusin sets by proving the following facts. (1) If U = x/N = {y ϵ 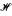 : ∀n ϵ ℕ(y < x/n)} for some x ϵ
: ∀n ϵ ℕ(y < x/n)} for some x ϵ 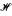 , then there exists a U-Lusin set of power κ if and only if there exists a Lusin set of the reals of power κ. (2) If U ≠ x/N but the coinitiality of U is ω, then there are no U-Lusin sets if CH fails. (3) Under ZFC there exists a nonstandard universe in which U-Lusin sets exist for every cut U with uncountable cofinality and coinitiality. (4) In any ω2-saturated nonstandard universe there are no U-Lusin sets for all cuts U except U = x/N.
, then there exists a U-Lusin set of power κ if and only if there exists a Lusin set of the reals of power κ. (2) If U ≠ x/N but the coinitiality of U is ω, then there are no U-Lusin sets if CH fails. (3) Under ZFC there exists a nonstandard universe in which U-Lusin sets exist for every cut U with uncountable cofinality and coinitiality. (4) In any ω2-saturated nonstandard universe there are no U-Lusin sets for all cuts U except U = x/N.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992


