Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-07T16:31:48.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Über ω-Unvollständigkeit in der Peano-Arithmetik

Published online by Cambridge University Press:  12 March 2014

G. Hasenjaeger
G. Hasenjaeger*
Affiliation:
Universität Münster
Get access Rights & Permissions [Opens in a new window]

Extract

Unter der Peano-Arithmetik verstehe ich im Folgenden eine über dem Prädikatenkalkül der ersten Stufe formalisierte Arithmetik der natürlichen Zahlen, in der als außerlogische Konstanten nur Symbole für die Null, die Nachfolgeroperation und die Gleichheitsbeziehung (die als mathematischer Grundbegriff aufgefaßt wird) vorkommen.

Ein Ausdruck H(c), in dem c die einzige freie Variable ist, heiße: ∀-defekt in Bezug auf ein (deduktives) System S, wenn (a) 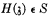für jede Ziffer 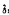, und (b) nicht ∀xH(x) ϵ S.

Im allgemeinen wird das deduktive System durch ein Axiomensystem in Verbindung mit einer Syntax gegeben sein. Auf diesen Fall soil die Redeweise sinngemäß übertragen werden.

Ein System S heiße ω-unvollständig, wenn es einen in Bezug auf S ∀-defekten Ausdruck gibt.

Ein Axiomensystem A heiße kategorisch, wenn beliebige absolute Modelle (s. Abschnitt IV) von A isomorph sind.

Die Kategorizität stellt eine gewisse Vollständigkeit des Axiomensystems dar. Daß solche Axiomensysteme ω-unvollstandig sein können (bzw. im Fall der ausdrucksreicheren Arithmetik nach Gödel sogar müssen), ist eben das Überraschende.

Ich werde im Folgenden für zwei kategorische Axiomensysteme der Peano-Arithmetik die ω-Unvollständigkeit in Bezug auf die Prädikatenlogik der ersten Stufe nachweisen. In beiden Fallen gelingt der Nachweis der ω-Unvollständigkeit durch Diskussion eines ∀-defekten Ausdrucks H(c).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 17 , Issue 2 , June 1952 , pp. 81 - 97
Copyright
Copyright © Association for Symbolic Logic 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

LITERATUR

[1]Ackermann, W., Untersuchungen über das Eliminationsproblem in der mathematischen Logik, Mathematische Annalen, vol. 110 (1934), pp. 390–413.CrossRefGoogle Scholar
[2]Gödel, K., Die Vollständigkeit der Axiome des logischen Funktionenkalküls, Monatshefte für Mathematik und Physik, vol. 37 (1930), pp. 349–360.CrossRefGoogle Scholar
[3]Gödel, K., Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I, Monatshefte für Mathematik und Physik, vol. 38 (1931), pp. 173–198.CrossRefGoogle Scholar
[4]Henkin, L., The completeness of formal systems, Dissertation, Princeton University, 1917.Google Scholar
[5]Hilbert-Ackermann, , Grundzüge der theoretischen Logik, 2. Aufl., Berlin 1938.CrossRefGoogle Scholar
[6]Hilbert-Bernays, , Grundlagen der Mathematik, I Berlin (1934), II (1939).Google Scholar
[7]Kemeny, J., Models of logical systems, in diesem Journal, vol. 13 (1948), pp. 16–30.Google Scholar
[8]Skolem, Th., Über die Nichtcharaklerisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschließlich Zahlenvariablen, Fundamenta mathematicae, vol. 23 (1934), pp. 150–161.CrossRefGoogle Scholar
[9]Tarski, A., Einige Betrachtungen über die Begriffe der ω-Widerspruchsfreiheit und der ω-Vollständigkeit, Monatshefte für Mathematik und Physik, vol. 40 (1933), pp. 97–112.CrossRefGoogle Scholar
[10]Tarski, A., Grundzüge des Systemenkalküls I, Fundamenta mathematicae, vol. 25 (1935), pp. 503–526.CrossRefGoogle Scholar
[11]Veblen, O., A system of axioms for geometry, Transactions of the American Mathematical Society, vol. 5 (1904), pp. 343–384.CrossRefGoogle Scholar