Article contents
Two-dimensional partial orderings: Recursive model theory
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper and the companion paper [9] we describe a number of contrasts between the theory of linear orderings and the theory of two-dimensional partial orderings.
The notion of dimensionality for partial orderings was introduced by Dushnik and Miller [3], who defined a partial ordering 〈A, R〉 to be n-dimensional if there are n linear orderings of A, 〈A, L1〉, 〈A, L2〉 …, 〈A, Ln〉 such that R = L1 ∩ L2 ∩ … ∩ Ln. Thus, for example, if Q is the linear ordering of the rationals, then the (rational) plane Q × Q with the product ordering (〈x1, y1〉 ≤Q×Q 〈x2, y2, if and only if x1 ≤ x2 and y1 ≤ y2) is 2-dimensional, since ≤Q×Q is the intersection of the two lexicographic orderings of Q × Q. In fact, as shown by Dushnik and Miller, a countable partial ordering is n-dimensional if and only if it can be embedded as a subordering of Qn.
Two-dimensional partial orderings have attracted the attention of a number of combinatorialists in recent years. A basis result recently obtained, independently, by Kelly [7] and Trotter and Moore [10], describes explicitly a collection 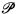 of finite partial orderings such that a partial ordering is a 2dpo if and only if it contains no element of
of finite partial orderings such that a partial ordering is a 2dpo if and only if it contains no element of 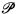 as a subordering.
as a subordering.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1980
References
BIBLIOGRAPHY
- 8
- Cited by


