Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T04:43:37.102Z Has data issue: false hasContentIssue false
  • English
  • Français

Transcendence of cardinals

Published online by Cambridge University Press:  12 March 2014

Gaisi Takeuti
Gaisi Takeuti*
Affiliation:
University of Illinois
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, by a function of ordinals we understand a function which is defined for all ordinals and each of whose value is an ordinal. In [7] (also cf. [8] or [9]) we defined recursive functions and predicates of ordinals, following Kleene's definition on natural numbers. A predicate will be called arithmetical, if it is obtained from a recursive predicate by prefixing a sequence of alternating quantifiers. A function will be called arithmetical, if its representing predicate is arithmetical.

The cardinals are identified with those ordinals a which have larger power than all smaller ordinals than a. For any given ordinal a, we denote by 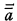the cardinal of a and by 2a the cardinal which is of the same power as the power set of a. Let χ be the function such that χ(a) is the least cardinal which is greater than a.

Now there are functions of ordinals such that they are easily defined in set theory, but it seems impossible to define them as arithmetical ones; χ is such a function. If we define χ in making use of only the language on ordinals, it seems necessary to use the notion of all the functions from ordinals, e.g., as in [6].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 30 , Issue 1 , March 1965 , pp. 1 - 7
Copyright
Copyright © Association for Symbolic Logic 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Gödel, K., The consistency of the axiom of choice and of the generalized continuum hypothesis with the axioms of set theory, Princeton, 1940.Google Scholar
[2]Levy, A., Axiom schemata of strong infinity in axiomatic set theory, Pacific Journal of Mathematics, vol. 10 (1960), pp. 223–238.CrossRefGoogle Scholar
[3]Mahlo, P., Über lineare transfinite Mengen. Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, vol. 63 (1911), pp. 187–225.Google Scholar
[4]Mahlo, P., Zur Theorie and Anwendung der ρ0-Zahlen. Berichte über die Verhandlungen der Königlich Sächsischen Gesellschaft der Wissenschaften zu Leipzig, vol. 64 (1912), pp. 108–112, vol. 65 (1913), pp. 268–282.Google Scholar
[5]Takeuti, G., Construction of the set theory from the theory of ordinal numbers. Journal of the Mathematical Society of Japan, vol. 6 (1954), pp. 196–220.CrossRefGoogle Scholar
[6]Takeuti, G., On the theory of ordinal numbers. Journal of the Mathematical Society of Japan, vol. 9 (1957), pp. 93–113.CrossRefGoogle Scholar
[7]Takeuti, G., On the recursive functions of ordinal numbers. Journal of the Mathematical Society of Japan, vol. 12 (1960), pp. 119–128.CrossRefGoogle Scholar
[8]Takeuti, G. and Kino, A., On hierarchies of predicates of ordinal numbers. Journal of the Mathematical Society of Japan, vol. 14 (1962), pp. 119–232.CrossRefGoogle Scholar
[9]Takeuti, G., A formalization of the theory of ordinal numbers. To appear in this Journal.Google Scholar