Published online by Cambridge University Press: 29 June 2016
Given a cardinal κ and a sequence 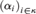 ${\left( {{\alpha _i}} \right)_{i \in \kappa }}$ of ordinals, we determine the least ordinal β (when one exists) such that the topological partition relationholds, including an independence result for one class of cases. Here the prefix “top” means that the homogeneous set must be of the correct homeomorphism class rather than the correct order type. The answer is linked to the nontopological pigeonhole principle of Milner and Rado.
${\left( {{\alpha _i}} \right)_{i \in \kappa }}$ of ordinals, we determine the least ordinal β (when one exists) such that the topological partition relationholds, including an independence result for one class of cases. Here the prefix “top” means that the homogeneous set must be of the correct homeomorphism class rather than the correct order type. The answer is linked to the nontopological pigeonhole principle of Milner and Rado.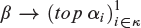 $$\beta \to \left( {top\,{\alpha _i}} \right)_{i \in \kappa }^1$$
$$\beta \to \left( {top\,{\alpha _i}} \right)_{i \in \kappa }^1$$