Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-20T00:57:28.920Z Has data issue: false hasContentIssue false
  • English
  • Français

There are 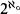many almost strongly minimal generalized n-gons that do not interpret an infinite group

Published online by Cambridge University Press:  12 March 2014

Mark J. Debonis  and
Ali Nesin
Mark J. Debonis
Affiliation:
Department of Mathematics, University of California, Irvine, CA 92717, USA
Ali Nesin
Affiliation:
Department of Mathematics, University of California, Irvine, CA 92717, USA Istanbul School for International Studies, Turkey Marmara Research Center—Tübİtak, Turkey
Get access Rights & Permissions [Opens in a new window]

Extract

Generalized n-gons are certain geometric structures (incidence geometries) that generalize the concept of projective planes (the nontrivial generalized 3-gons are exactly the projective planes).

In a simplified world, every generalized n-gon of finite Morley rank would be an algebraic one, i.e., one of the three families described in [9] for example. To our horror, John Baldwin [2], using methods discovered by Hrushovski [7], constructed ℵ1-categorical projective planes which are not algebraic. The projective planes that Baldwin constructed fail to be algebraic in a dramatic way.

Indeed, every algebraic projective plane over an algebraically closed field is Desarguesian [12]. In particular, an algebraically closed field (isomorphic to the base field) can be interpreted in every one of them. However, in the projective planes that Baldwin constructed, one cannot even interpret an infinite group.

In this article we show that the same phenomenon occurs for the generalized n-gons if n ≥ 3 is an odd integer. For each such n we construct 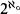many nonisomorphic generalized n-gons of finite Morley rank that do not interpret an infinite group. As one may expect, our method is inspired by Hrushovski and Baldwin, and we follow Baldwin's line of approach. Quite often our proofs are a verification of the fact that the proofs of Baldwin [2] for n = 3 carry over to an arbitrary positive odd integer n (which is sometimes far from being obvious). As in [2], we begin by defining a certain collection of finite graphs K* and a binary relation ≤ on these graphs. We show that (K*, ≤) satisfies the amalgamation property.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 2 , June 1998 , pp. 485 - 508
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baldwin, J. T., αT is finite for ℵ1-categorical T, Transactions of the American Mathematical Society, vol. 181 (1973), pp. 37–51.Google Scholar
[2] Baldwin, J. T., An almost strongly minimal non-desarguesian projective plane, Transactions of the American Mathematical Society, vol. 342 (1994), no. 2, pp. 695–711.Google Scholar
[3] Borovik, A. and Nesin, A., Groups of finite Morley rank, Oxford University Press, 1994.Google Scholar
[4] Clapham, C. R. J., Flockhart, A., and Sheehan, J., Graphs without four-cycles, Journal of Graph Theory, vol. 13 (1989), no. 1, pp. 29–47.10.1002/jgt.3190130107Google Scholar
[5] Feit, W. and Higman, G., The nonexistence of certain generalized polygons, Journal of Algebra, vol. 1 (1964), pp. 114–131.Google Scholar
[6] Herwig, B., Weight ω in stable theories with few types, this Journal, vol. 60 (1995), pp. 353–373.Google Scholar
[7] Hrushovski, E., A new strongly minimal set, Annals of Pure and Applied Logic, vol. 62 (1993), pp. 147–166.Google Scholar
[8] Hughes, D. R. and Piper, F. C., Projective planes, Springer-Verlag, Berlin and New York, 1973.Google Scholar
[9] Kramer, L. and Tent, K., Algebraic polygons, to be published in Journal of Algebra.Google Scholar
[10] Nesin, A., On bad-groups, bad-fields and pseudo-planes, this Journal, vol. 56 (1991), pp. 915–931.Google Scholar
[11] Shelah, S., Universal classes, Part 1, Classification theory (Baldwin, J., editor), Lecture Notes in Mathematics, no. 1292, Springer-Verlag, Berlin and New York, 1987, pp. 264–419.Google Scholar
[12] Strambach, K., Algebraische Geometrien, Rendiconti del Seminario Matematico delta Università de Padova, vol. 53 (1975), pp. 165–210.Google Scholar
[13] Tits, J., Buildings of spherical type and finite BN-pairs, Lecture Notes in Mathematics, no. 386, Springer-Verlag, Berlin and New York, 1974.Google Scholar
[14] Tits, J., Endliche Spiegelungsgruppen, dies als Weylgruppen auftreten, Inventiones Mathematicae, vol. 43 (1977), pp. 283–295.Google Scholar