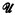Let be the class of recursively enumerable (r.e.) sets with infinite complements. A set M ϵ 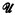is maximal if every superset of M which is in 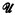is only finitely different from M. In [1] Friedberg shows that maximal sets exist, and it is an easy consequence of this fact that every non-simple set in 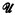has a maximal superset. The natural question which arises is whether or not this is also true for every simple set (Ullian [2]). In the present paper this question is answered negatively. However, the main concern of this paper is with demonstrating, and developing a few consequences of, what might be called the “density” of hyperhypersimple sets.