Article contents
A theorem about infinite-valued sentential logic1
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we shall use a logic with truth values ranging over all the real numbers x such that 0 ≦ x ≦ 1.1 will be “complete truth” and 0 will be “complete falsity.” The primitive sentential connectives are ‘⊃’ and ‘∼’; other connectives are ‘∨’ and ‘·’. Assume that ‘p’ and ‘q’ are sentential variables, whose truth values are respectively x and y. Then
1.1. ‘p ⊃ q’ has the value min(1 − x + y, 1),
1.2. ‘∼p’ has the value 1 − x,
1.3. ‘p∨q’ has the value max(x, y), and
1.4. ‘p·q’ has the value min (x, y).
‘∨’ and ‘·’ can be defined as follows:
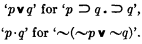
It is the purpose of this paper to prove a theorem which will be stated in the next section. The following symbolism and convention will be used throughout the paper:
S is a logical formula.
ν (S) is the value of S.
‘p’, ‘pi1, ’p2, …, ‘q’, are sentential variables.
ν(p) = x and ν(x1) = x1, etc.
ν(S) = σ and ν(S1) = σ1, etc.
If S contains the sentential variables ‘p1’, ‘p2’, …, then we write for S, S(p1, P2, …). Also ν{S(p1, p2, …)) = σ(x1, x2, …).
A logical formula is defined in the usual manner. 1. A sentential variable is a logical formula; 2. if S is a logical formula then ·S is a logical formula; and 3. if S and S′ are logical formulae then (S ⊃ S′) is a logical formula.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1951
Footnotes
I am indebted to Maxwell Rosenlicht and to Chandler Davis of Harvard University for their indispensable advice and aid in the writing of this paper.
References
2 The reader will note that to this problem in infinite-valued logic corresponds the problem in two-valued logic of constructing a logical formula for a given truth table.
3 The idea for this section was suggested by Maxwell Rosenlicht of Harvard University.
4 Łukasiewicz, Jan and Tarski, Alfred, Untersuchungen über den Aussagenkalkul, Comptes rendus des séances de la Société des Sciences et des Lettres, Cl. Ill, vol. 23 (1930), pp. 30–50Google Scholar. They write ‘Cpq’ and ‘Np’ for ‘p ⊃ q’ and ‘∼p’, respectively. The definition which I use for L-sub-ℵ0 is not the definition which is originally given, but is the definition appearing in “Satz 16”.
5 Loc cit.
6 Axiom schemes for m-valued prepositional calculus, this Journal, vol. 10 (1945), pp. 61–82Google Scholar. We are referring here to the functionally incomplete logic of pp. 62–65. (The reader will also notice the similarity between what is accomplished in these pages, namely the definition of Jk(P) and the proof that it has a certain desired truth evaluation, and what is accomplished in section 3 of the present paper.)
- 210
- Cited by


