Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brendle, Jörg
1996.
Generic constructions of small sets of reals.
Topology and its Applications,
Vol. 71,
Issue. 2,
p.
125.
Scheepers, Marion
1998.
Combinatorics of open covers IV: subspaces of the Alexandroff double of the unit interval.
Topology and its Applications,
Vol. 83,
Issue. 1,
p.
63.
Bartoszynski, Tomek
and
Shelah, Saharon
2001.
Continuous images of sets of reals.
Topology and its Applications,
Vol. 116,
Issue. 2,
p.
243.
Rupprecht, Nicholas
2010.
Relativized Schnorr tests with universal behavior.
Archive for Mathematical Logic,
Vol. 49,
Issue. 5,
p.
555.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
383.
Hrušák, Michael
Wohofsky, Wolfgang
and
Zindulka, Ondřej
2016.
Strong measure zero in separable metric spaces and Polish groups.
Archive for Mathematical Logic,
Vol. 55,
Issue. 1-2,
p.
105.
Halbeisen, Lorenz J.
2017.
Combinatorial Set Theory.
p.
503.
Cardona, Miguel A.
Mejía, Diego A.
and
Rivera-Madrid, Ismael E.
2022.
The covering number of the strong measure zero ideal can be above almost everything else.
Archive for Mathematical Logic,
Vol. 61,
Issue. 5-6,
p.
599.
Cardona, Miguel A.
Klausner, Lukas Daniel
and
Mejía, Diego A.
2024.
Continuum many different things: Localisation, anti-localisation and Yorioka ideals.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 7,
p.
103453.
CHAPMAN, NICK STEVEN
and
SCHÜRZ, JOHANNES PHILIPP
2024.
STRONG MEASURE ZERO SETS ON FOR INACCESSIBLE.
The Journal of Symbolic Logic,
p.
1.
FISCHER, VERA
and
SWITZER, COREY BACAL
2024.
TIGHT EVENTUALLY DIFFERENT FAMILIES.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 2,
p.
697.
Cardona, Miguel A.
and
Mejía, Diego A.
2025.
More about the cofinality and the covering of the ideal of strong measure zero sets.
Annals of Pure and Applied Logic,
Vol. 176,
Issue. 4,
p.
103537.


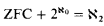 :
: