Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T20:19:18.236Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong convergence in finite model theory

Published online by Cambridge University Press:  12 March 2014

Wafik Boulos Lotfallah
Wafik Boulos Lotfallah*
Affiliation:
Department of Engineering Mathematics and Physics, Faculty of Engineering, Cairo University, Cairo, Egypt, 11451, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In [9] we introduced a new framework for asymptotic probabilities, in which a σ-additive measure is defined on the sample space of all sequences 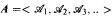of finite models, where the universe of 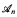, is {1,2,…,n}. In this framework we investigated the strong 0-1 law for sentences, which states that each sentence either holds in 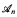eventually almost surely or fails in 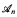eventually almost surely.

In this paper we define the strong convergence law for formulas, which carries over the ideas of the strong 0-1 law to formulas with free variables, and roughly states that for each formula ϕ(x), the fraction of tuples a in 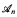, which satisfy the formula ϕ(x), almost surely has a limit as n tends to infinity.

We show that the infinitary logic with finitely many variables has the strong convergence law for formulas for the uniform measure, and further characterize the measures on random graphs for which the strong convergence law holds.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 1083 - 1092
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Compton, K. J., 0-1 laws in logic and combinatorics, NATO Advanced Study Institute on Algorithms and Order, 1987, pp. 353–383.Google Scholar
[2]Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 17–21.Google Scholar
[3]Glebskii, Y. V, Kogan, D. I., Liogonki, M. I., and Talanov, V. A., Range and degree of readability of formulas in the restricted predicate calculus. Cybernetics, vol. 5 (1969), pp. 142–154.CrossRefGoogle Scholar
[4]Halmos, P. R., Measure Theory, Springer-Verlag, 1974.Google Scholar
[5]Hella, L., Kolaitis, P. G., and Luosto, K., Almost everywhere equivalence of logics in finite model theory, The Bulletin of Symbolic Logic, vol. 2 (1996), no. 4, pp. 422–443.CrossRefGoogle Scholar
[6]Keisler, H. J., Hyperfinite model theory, Logic Symposium'76 (Gandy, and Hyland, , editors), North Holland, 1977.Google Scholar
[7]Knyazev, V. V., Zero-One law for an extension of first-order predicate language, Kibernetika, (1990), no. 2. pp. 110–113, 03–April.Google Scholar
[8]Kolaitis, P. G. and Vardi, M. Y., Infinitary logics and 0-1 laws, Information and Computation, vol. 98 (1992), pp. 258–294, special issue: selection from the 5th, annual IEEE Symposium on Logic in Computer Science.CrossRefGoogle Scholar
[9]Lotfallah, W. B., Strong 0-1 laws in finite model theory, this Journal, vol. 65 (2000), no. 4, pp. 1686–1704.Google Scholar
[10]Luczak, T. and Spencer, J., When does the zero-one law hold, Journal of the American Mathematical Society, vol. 4 (1991), no. 3, pp. 451–468.CrossRefGoogle Scholar
[11]Shelah, S. and Spencer, J., Zero-one laws for sparse random graphs, Journal of the American Mathematical Society, vol. 1 (1988), pp. 97–115.CrossRefGoogle Scholar
[12]Williams, D., Probability with Martingales, Cambridge University Press, 1991.CrossRefGoogle Scholar