Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T01:30:17.911Z Has data issue: false hasContentIssue false
  • English
  • Français

A stochastic interpretation of propositional dynamic logic: expressivity

Published online by Cambridge University Press:  12 March 2014

Ernst-Erich Doberkat
Ernst-Erich Doberkat*
Affiliation:
Chair for Software Technology and Department of Mathematics, Technische Universität Dortmund, 44227 Dortmund, Germany, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a probabilistic interpretation of Propositional Dynamic Logic (PDL). We show that logical and behavioral equivalence are equivalent over general measurable spaces. This is done first for the fragment of straight line programs and then extended to cater for the nondeterministic nature of choice and iteration, expanded to PDL as a whole. Bisimilarity is also discussed and shown to be equivalent to logical and behavioral equivalence, provided the base spaces are Polish spaces. We adapt techniques from coalgebraic stochastic logic and point out some connections to Souslin's operation 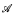from descriptive set theory. This leads to a discussion of complete stochastic Kripke models and model completion, which permits an adequate treatment of the test operator.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 2 , June 2012 , pp. 687 - 716
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Blackburn, P., de Rijke, M., and Venema, Y., Modal logic, Cambridge Tracts in Theoretical Computer Science, vol. 53, Cambridge University Press, Cambridge, UK, 2001.CrossRefGoogle Scholar
[2] Blackburn, P. and van Benthem, J., Modal logic: A semantic perspective, Handbook of modal logic (Blackburn, P. et al., editors), Elsevier, Amsterdam, 2007, pp. 1–84.Google Scholar
[3] Bonanno, G., Modal logic and game theory—two alternative approaches, Risk Decision and Policy, vol. 7 (2002), pp. 309–324.Google Scholar
[4] Desharnais, J., Edalat, A., and Panangaden, P., Bisimulation of labelled Markov processes, Information and Computation, vol. 179 (2002), no. 2, pp. 163–193.Google Scholar
[5] Doberkat, E.-E., An analysis of Floyd's algorithm for heapconstruction, Information and Control, vol. 61 (1984), pp. 114–131.CrossRefGoogle Scholar
[6] Doberkat, E.-E., Stochastic relations: congruences, hisimulations and the Hennessy–Milner theorem, SIAM Journal on Computing, vol. 35 (2006), no. 3, pp. 590–626.CrossRefGoogle Scholar
[7] Doberkat, E.-E., Kleisli morphisms and randomized congruences for the Giry monad, Journal of Pure and Applied Algebra, vol. 211 (2007), pp. 638–664.CrossRefGoogle Scholar
[8] Doberkat, E.-E., Stochastic relations. Foundations for Markov transition systems, Chapman & Hall/CRC Press, Boca Raton, New York, 2007.Google Scholar
[9] Doberkat, E.-E., Stochastic coalgebraic logic, EATCS Monographs in Theoretical Computer Science, Springer-Verlag, 2009.Google Scholar
[10] Doberkat, E.-E., A note on the coalgebraic interpretation of game logic, Rendiconti dell'Istituto di Matematica dell'Università di Trieste, vol. 42 (2010), pp. 191–204.Google Scholar
[11] Doberkat, E.-E. and Kurz, A., Special issue on coalgebraic logic, Mathematical Structures in Computer Science, vol. 21 (2011 ).Google Scholar
[12] Doberkat, E.-E. and Schubert, Ch., Coalgebraic logic over general measurable spaces—a survey, Mathematical Structures in Computer Science, vol. 21 (2011), pp. 175–234, special issue on coalgebraic logic.Google Scholar
[13] Doberkat, E.-E. and Srivastava, S. M., Measurable selections, transition probabilities and Kripke models, Technical Report 185. Chair for Software Technology, Technische Universität Dortmund, 05 2010.Google Scholar
[14] Giry, M., A categorical approach to probability theory, Categorical aspects of topology and analysis, Lecture Notes in Mathematical, vol. 915, Springer-Verlag, Berlin, 1981, pp. 68–85.Google Scholar
[15] Halmos, P. R., Measure theory, Van Nostrand Reinhold, New York, 1950.Google Scholar
[16] Harrenstein, B. P., der Hoek, W. van, Meyer, J.-J. Ch., and Witteveen, C., A modal characterization of Nash equilibrium, Fundamenta Informaticae, vol. 57 (2003), pp. 281–321.Google Scholar
[17] Hennessy, M. and Milner, R., On observing nondeterminism and concurrency, Proceedings of ICALP'80, Lecture Notes in Computer Science, vol. 85, Springer-Verlag, Berlin, 1980, pp. 395–409.Google Scholar
[18] Kechris, A. S., Classical descriptive set theory, Graduate Texts in Mathematics, Springer-Verlag, Berlin, 1994.Google Scholar
[19] Knuth, D. E., The art of computer programming. Volume III, Sorting and searching, Addison-Wesley, Reading, MA, 1973.Google Scholar
[20] Kurz, A., Specifying coalgebras with modal logic, Theoretical Computer Science, vol. 260 (2001), pp. 119–138.Google Scholar
[21] Lubin, A., Extensions of measures and the von Neumann selection theorem, Proceedings of the American Mathematical Society, vol. 43 (1974), no. 1, pp. 118–122.Google Scholar
[22] Parikh, R., The logic of games and its applications, Topics in the theory of computation (Karpinski, M. and van Leeuwen, J., editors), vol. 24, Elsevier, 1985, pp. 111–140.Google Scholar
[23] Pauly, M., Game logic far game theorists, Technical Report INS-R0017, CWI, Amsterdam, 2000.Google Scholar
[24] Pauly, M. and Parikh, R., Game logic—an overview, Studia Logica, vol. 75 (2003), no. 2, pp. 165–182.Google Scholar
[25] Rutten, J. J. M. M., Universal coalgebra: a theory of systems, Theoretical Computer Science, vol. 249 (2000), no. 1, pp. 3–80, special issue on modern algebra and its applications.Google Scholar
[26] Schröder, L. and Pattinson, D., Modular algorithms for heterogeneous modal logics, Proceedings of ICALP, Lecture Notes in Computer Science, vol. 4596, 2007, pp. 459–471.Google Scholar
[27] Srivastava, S. M., A course on Borei sets, Graduate Texts in Mathematics, Springer-Verlag, Berlin, 1998.Google Scholar
[28] Terraf, P. Sànchez, Unprovability of the logical characterization of bisimulation, Information and Computation, vol. 209 (2011), no. 7, pp. 1048–1056.Google Scholar
[29] der Hoek, W. van and Pauly, M., Modal logic for games and information, Handbook of modal logic (Blackburn, P., van Benthem, J., and Wolter, F., editors), Studies in Logic and Practical Reasoning, vol. 3, Elsevier, Amsterdam, 2007, pp. 1077–1148.Google Scholar