Article contents
Stability theory and set existence axioms
Published online by Cambridge University Press: 12 March 2014
Extract
A series of investigations started by H. Friedman ([5], [6]) and pursued by him, by S. Simpson, and by others (see [7], [16] and the references there) had the objective of determining what are precisely the set existence axioms needed for proving theorems of “ordinary” mathematics. The study centered around 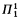 -CA0 (for “
-CA0 (for “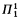 -Comprehension Axiom”), a fragment of second order arithmetic in which the main body of “ordinary” mathematics can be comfortably developed (of course, after a suitable encoding of the various concepts into numbers and sets of numbers). The main question is always this: given a theorem τ provable in
-Comprehension Axiom”), a fragment of second order arithmetic in which the main body of “ordinary” mathematics can be comfortably developed (of course, after a suitable encoding of the various concepts into numbers and sets of numbers). The main question is always this: given a theorem τ provable in 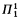 -CA0, do we need all of
-CA0, do we need all of 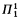 -CA0, or, maybe, is τ provable in a weaker subsystem? A surprisingly simple pattern emerged: there seem to be just five important systems, denoted (in order of increasing strength) RCA0, WKL0, ACA0, ATR0 and
-CA0, or, maybe, is τ provable in a weaker subsystem? A surprisingly simple pattern emerged: there seem to be just five important systems, denoted (in order of increasing strength) RCA0, WKL0, ACA0, ATR0 and 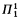 -CA0, such that in most cases, whenever an ordinary mathematical theorem τ is provable in
-CA0, such that in most cases, whenever an ordinary mathematical theorem τ is provable in 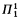 -CA0, it is either provable in RCA0 or it is equivalent to one, call it S, of the other four systems, the proof of the equivalence being done in one of the systems which is weaker than S (most typically, RCA0 or ACA0). This very interesting phenomenon—or “theme” as it was called by Friedman—has been verified for many instances in the realm of analysis and algebra (cf. the references above and the forthcoming book [17]). It is the purpose of this paper to do the same for a particular branch of model theory, namely stability theory.
-CA0, it is either provable in RCA0 or it is equivalent to one, call it S, of the other four systems, the proof of the equivalence being done in one of the systems which is weaker than S (most typically, RCA0 or ACA0). This very interesting phenomenon—or “theme” as it was called by Friedman—has been verified for many instances in the realm of analysis and algebra (cf. the references above and the forthcoming book [17]). It is the purpose of this paper to do the same for a particular branch of model theory, namely stability theory.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
- 4
- Cited by


