Published online by Cambridge University Press: 12 March 2014
Beginning with Ramsey's theorem of 1930, combinatorists have been intrigued with the notion of large cardinals satisfying partition relations. Years of research have established the smaller ones, weakly ineffable, Erdös, Jonsson, Rowbottom and Ramsey cardinals to be among the most interesting and important large cardinals in set theory. Recently, cardinals satisfying more powerful infinite-exponent partition relations have been examined with growing interest. This is due not only to their inherent qualities and the fact that they imply the existence of other large cardinals (Kleinberg [2], [3]), but also to the fact that the Axiom of Determinacy (AD) implies the existence of great numbers of such cardinals (Martin [5]).
That these properties are more often than not inconsistent with the full Axiom of Choice (Kleinberg [4]) somewhat increases their charm, for the theorems concerning them tend to be a little odd, and their proofs, circumforaneous. The properties are, as far as anyone knows, however, consistent with Dependent Choice (DC).
Our basic theorem will be the following: If k > ω and k satisfies k→(k)k then the least cardinal δ such that 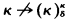 has a δ-additive, uniform ultrafilter. In addition, if ACω is assumed, we will show that δ is greater than ω, and hence a measurable cardinal. This result will be strengthened somewhat when we prove that for any k, δ, if
has a δ-additive, uniform ultrafilter. In addition, if ACω is assumed, we will show that δ is greater than ω, and hence a measurable cardinal. This result will be strengthened somewhat when we prove that for any k, δ, if 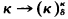 then
then  .
.