Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T23:19:44.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Some anomalies in Fitch's system QD

Published online by Cambridge University Press:  12 March 2014

M. W. Bunder  and
Jonathan P. Seldin
M. W. Bunder
Affiliation:
Oxford University, Oxfordshire, England
Jonathan P. Seldin
Affiliation:
Oxford University, Oxfordshire, England
Get access Rights & Permissions [Opens in a new window]

Extract

This note shows that the argument used in the proof of the inconsistency of Curry's system 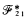(see [1]) can also be applied to Fitch's system QD (see [3, Chapter 6]). As one vital rule of 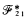is not present in QD this argument does not lead to an actual contradiction, but it does lead to a theorem which is not a proposition if the system is consistent.

The method used below is that of [2], which is simpler than that of [1].

The axioms and rules of QD that we require are also present in [1] and [2] provided that Fitch's D is replaced by H. These axioms and rules are the following:

DD int: ⊦ D(Da),

m p: If ⊦ a ⊃ b2 and ⊦ a then ⊦ b, and

res imp int: If a ⊦ b then Da ⊦ a ⊃ b.

Let a be arbitrary and let G be [x](Dx ⊃ (x ⊃ a)). Then let X be BWBG(BWBG). We then have the following proof:

Thus, we have ⊦ X. Now suppose we also had ⊦ DX. Then by the method of the innermost subproof in the above proof, we would have ⊦ a, and since a is

arbitrary the system would be inconsistent. Hence, if QD is consistent, we do not have ⊦ DX, and so X is a theorem which is not a proposition.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 2 , June 1978 , pp. 247 - 249
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bunder, M. W., The inconsistency of , this Journal, vol. 41 (1976), pp. 467–468.Google Scholar
[2]Bunder, M. W. and Meyer, R. K., On the inconsistency of systems similar to , this Journal, vol. 43 (1978), pp. 1–2.Google Scholar
[3]Fitch, Frederic B., Elements of combinatory logic, Yale University Press, New Haven and London, 1974.Google Scholar
[4]Fitch, Frederic B., An extension of CΔ (to appear).Google Scholar
[5]Fitch, Frederic B., Excluded middle and the paradoxes, abstract, Meeting of the Association for Symbolic Logic, New York, 1975, this Journal, vol. 42 (1977), pp. 148–149.Google Scholar