Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T12:23:57.062Z Has data issue: false hasContentIssue false
  • English
  • Français

A sheaf representation and duality for finitely presented Heyting algebras

Published online by Cambridge University Press:  12 March 2014

Silvio Ghilardi  and
Marek Zawadowski
Silvio Ghilardi
Affiliation:
Dipartimento di Matematica, Università degli Studi di Milano, Via C. Saldini 50, 20133 Milano, Italy, E-mail: [email protected]
Marek Zawadowski
Affiliation:
Instytut Matematyki, Uniwersytet Warszawski, UL. S.Banacha 2, 00-913 Warszawa, Poland, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

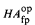A. M.Pitts in [Pi] proved that is a bi-Heyting category satisfying the Lawvere condition. We show that the embedding Φ: 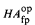→ Sh(P0, J0) into the topos of sheaves, (P0 is the category of finite rooted posets and open maps, J0 the canonical topology on P0) given by H ↦ HA(H, 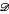(−)) : P0 → Set preserves the structure mentioned above, finite coproducts, and subobject classifier; it is also conservative. This whole structure on 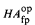can be derived from that of Sh(P0, J0) via the embedding Φ. We also show that the equivalence relations in 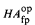are not effective in general. On the way to these results we establish a new kind of duality between 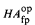and a category of sheaves equipped with certain structure defined in terms of Ehrenfeucht games. Our methods are model-theoretic and combinatorial as opposed to proof-theoretic as in [Pi].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 3 , September 1995 , pp. 911 - 939
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[SGA4]Artin, M., Grothendieck, A., and Verdier, J. L., Séminaire de géométrie algébrique 4, Lecture Notes in Mathematics, No. 269, Springer, 1972.Google Scholar
[Be]Bellissima, F., Finitely generatedfree Hey ting algebras, this Journal, vol. 51 (1986), pp. 152–165.Google Scholar
[Fi1]Fine, K., Logics containing K4, Part I, this Journal, vol. 34 (1974), pp. 31–42.Google Scholar
[Fi2]Fine, K., Logics containing K4, Part II, this Journal, vol. 50 (1985), pp. 619–651.Google Scholar
[Ga]Gabbay, D. M., Semantical investigations in Heyting intuitionistic logic, Synthese Library 148, Reidel, 1981.CrossRefGoogle Scholar
[GU]Gabriel, P. and Ulmer, F., Lokal prasentierbare kategorien, Lecture Notes in Mathematics, No. 221, Springer, 1971.CrossRefGoogle Scholar
[Gh]Ghilardi, S., Free Heyting algebras as bi-Heyting algebras, Mathematical Reports of Academy of Sciences of Canada, vol. XIV (1992), no. 6, pp. 240–244.Google Scholar
[Gh1]Ghilardi, S., An algebraic theory of normal forms, Annals of Pure and Applied Logic, vol. 71 (1995), pp. 189–245.CrossRefGoogle Scholar
[GG]Gleit, Z. and Goldfarb, W., Characters and fixed points in provability logic, Notre Dame Journal of Formal Logic, vol. 31 (1990), pp. 26–36.Google Scholar
[PTJ]Johnstone, P. T., Stone spaces, Cambridge University Press, 1982.Google Scholar
[La]Lawvere, F. W., Intrinsic co-Heyting boundaries and the Leibniz rule in certain toposes, Category theory, Proceedings Como 1990, Springer Lecture Notes in Mathematics, No. 1488, 1991, pp. 279–281.CrossRefGoogle Scholar
[CWM]MacLane, S., Categories for the working mathematician, Springer, Berlin, 1971.Google Scholar
[Ma]Makkai, M., Duality and definability in first order logic, Memoirs, vol. 503, American Mathematical Society, 1993.Google Scholar
[MR]Makkai, M. and Reyes, G. E., First order categorical logic, Lecture Notes in Mathematics, No. 611, Springer, 1977.CrossRefGoogle Scholar
[MR 1]Reyes, G. E., Completenessresultsfor intuitionistic and modal logic in a categorical setting, preprint, Université de Montréal, 1992.Google Scholar
[Pi]Pitts, A. M., On an interpretation of second order quantification in first order intuitionistic propositional logic, this Journal, vol. 57 (1992), pp. 33–52.Google Scholar
[Pr]Priestley, H. A., Representation of distributive lattices by means of ordered Stone spaces, The Bulletin of the London Mathematical Society, vol. 2 (1970), pp. 186–190.CrossRefGoogle Scholar
[Ry]Rybakov, V. V., Admissibility of inference rules with parameters in intuitionistic logic and intuitionistic Kripke models, Doklady Akademii Nauk, vol. 312 (1990),pp. 42–45.Google Scholar
[Sha]Shavrukov, V. Yu., Subalgebras of diagonalizable algebras of theories containing arithmetic, Dissertationesmathematicae, vol. CCCXXIII, Polska Akademia Nauk, Instytut Matematyczny, Warsaw, 1993.Google Scholar
[Ur]Urquhart, A., Free Heyting algebras, Algebra Universalis, vol. 3 (1973), pp. 94–97.CrossRefGoogle Scholar
[vD]van Dalen, D., Intuitionistic logic, Handbook of philosophical logic (Gabbay, D. M. and Günther, C., editors), vol. III, Reidel, 1986, pp. 225–339.CrossRefGoogle Scholar
[Za]Zawadowski, M. W., Descent and duality, Annals of Pure and Applied Logic, vol. 71 (1995), pp. 131–188.CrossRefGoogle Scholar