Article contents
SEPARABLY CLOSED VALUED FIELDS: QUANTIFIER ELIMINATION
Published online by Cambridge University Press: 12 August 2016
Abstract
It is proved in this article that the theory of separably closed nontrivially valued fields of characteristic p > 0 and imperfection degree e > 0 (e ≤ ∞) has quantifier elimination in the language 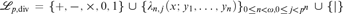 ${{\cal L}_{p,{\rm{div}}}} = \{ + , - , \times ,0,1\} \cup {\{ {\lambda _{n,j}}(x;{y_1}, \ldots ,{y_n})\} _{0 \le n < \omega ,0 \le j < {p^n}}} \cup \{ |\}$; in particular, when e is finite, the corresponding theory has quantifier elimination in the language
${{\cal L}_{p,{\rm{div}}}} = \{ + , - , \times ,0,1\} \cup {\{ {\lambda _{n,j}}(x;{y_1}, \ldots ,{y_n})\} _{0 \le n < \omega ,0 \le j < {p^n}}} \cup \{ |\}$; in particular, when e is finite, the corresponding theory has quantifier elimination in the language 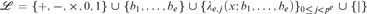 ${\cal L} = \{ + , - , \times ,0,1\} \cup \{ {b_1}, \ldots ,{b_e}\} \cup {\{ {\lambda _{e,j}}(x;{b_1}, \ldots ,{b_e})\} _{0 \le j < {p^e}}} \cup \{ |\}$.
${\cal L} = \{ + , - , \times ,0,1\} \cup \{ {b_1}, \ldots ,{b_e}\} \cup {\{ {\lambda _{e,j}}(x;{b_1}, \ldots ,{b_e})\} _{0 \le j < {p^e}}} \cup \{ |\}$.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2016
References
REFERENCES
- 2
- Cited by


