Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Glymour, Clark
1970.
Theoretical Realism and Theoretical Equivalence.
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association,
Vol. 1970,
Issue. ,
p.
275.
Baur, Walte
1974.
�ber rekursive Strukturen.
Inventiones Mathematicae,
Vol. 23,
Issue. 2,
p.
89.
Erš, Ju. L.
1977.
Theorie Der Numerierungen III.
Mathematical Logic Quarterly,
Vol. 23,
Issue. 19-24,
p.
289.
Mostowski, Andrzej
1979.
Foundational Studies Selected Works.
Vol. 93,
Issue. ,
p.
1.
Smoryński, Craig
1982.
The finite inseparability of the first-order theory of diagonalisable algebras.
Studia Logica,
Vol. 41,
Issue. 4,
p.
347.
van Benthem, Johan
1982.
The logical study of science.
Synthese,
Vol. 51,
Issue. 3,
p.
431.
Compton, Kevin J.
1989.
Algorithms and Order.
p.
353.
Fagin, Ronald
1990.
ICDT '90.
Vol. 470,
Issue. ,
p.
1.
Compton, Kevin J.
and
Ward Henson, C.
1990.
A uniform method for proving lower bounds on the computational complexity of logical theories.
Annals of Pure and Applied Logic,
Vol. 48,
Issue. 1,
p.
1.
Hazewinkel, M.
1992.
Encyclopaedia of Mathematics.
p.
1.
Fagin, Ronald
1993.
Finite-model theory - a personal perspective.
Theoretical Computer Science,
Vol. 116,
Issue. 1,
p.
3.
Grumbach, Stéphane
Su, Jianwen
and
Tollu, Christophe
1995.
Logic and Computational Complexity.
Vol. 960,
Issue. ,
p.
426.
Skornyakov, L. A.
Mysovskikh, I. P.
Talalyan, A. A.
Solomentsev, E. D.
Sveshnikov, A. G.
Chuyanov, V. A.
Shmel’kin, A. L.
Andrunakievich, V. A.
Minlos, R. A.
Bulota, K. Yu.
Kuz’min, L. V.
Mineev, M. P.
Sevast’yanov, B. A.
Cnentsov, N. N.
Dobrushin, R. L.
Prelov, V. V.
Prokhorov, Yu. V.
Yaglom, A. M.
Kolchin, V. F.
Pagurova, V. I.
Borovkov, A. A.
Nikulin, M. S.
Popova, T. Yu.
Ivanova, O. A.
Popov, V. L.
Govorov, V. E.
Fedoryuk, M. V.
D’yakonov, E. G.
Dolzhenko, K. P.
Kulikov, Viktor S.
Sullivan, D.
Kudryavtsev, L. D.
Kulikov, Val. S.
Rapinchuk, A. S.
Malyshev, A. V.
Dellacherie, C.
Babich, V. M.
Prokhorov, A. V.
Rozov, N. Kh.
Fife, P. C.
Gudkov, D. A.
Ponomarev, D. A.
Plisko, V. E.
Stepanov, S. A.
Golubov, B. I.
Artemov, S. N.
Millionshchikov, K. M.
Millionshchikov, V. M.
Belyakin, N. V.
Dushskiĭ, V. A.
Rousseeuw, P. J.
Domanskiĭ, V. K.
Goncharov, S. S.
Degtev, A. N.
Tankeev, S. G.
Grishin, V. N.
Millwnshchikov, V. M.
Alekseevskiĭ, D. V.
Shevrin, L. N.
Turchin, V. F.
Arkhangelskiĭ, A. V.
Vinberg, E. B.
Dolzhenko, E. P.
Vil’yams, N. N.
Solomentsev, E. V.
Buevich, V. A.
Vapnyarskiĭ, I. B.
Vladimirov, U. A.
Viil’yams, N. N.
Ivanov, A. B.
Danilov, V. I.
Shevnn, L. N.
Terekhin, A. P.
Ilyashenko, Yu. S.
Skiĭ, A. V. Arkhangel
Volkov, J. J.
Platonov, V. P.
Volkov, I. I.
Arsenin, V. Ya.
Tikhonov, A. N.
Mishchenko, A. S.
Norden, A. P.
Mikhalev, A. V.
Sklyarenko, E. G.
Sokolov, D. D.
Ruzmaĭkin, A. A.
Nikolaev, E. S.
Karpova, N. A.
Yablonskiĭ, S. V.
Belyaev, Yu. K.
Gnedenko, B. V.
Sevast’yanov, V. A.
Anikin, S. A.
Tsalenko, M. Sh.
Onishchik, A. L.
Rudakov, A. N.
Ringel, C. M.
Gluskin, L. M.
Lyapin, E. S.
Shtern, A. I.
Roĭter, A. V.
Nagornyĭ, N. M.
Merzlyakov, Yu. I.
Golubov, E. A.
Yuzhakov, A. P.
Sobolev, V. I.
Kuzmm, L. V.
Voĭtseknovskiĭ, M. I.
Butenin, N. V.
Bryuno, A. D.
Proskuryakov, I. V.
Nakhushev, A. M.
Arkhangel’skiĭ, A. V.
Malakhovskiĭ, V. S.
Tonkov, E. L.
Sidorov, L. A.
Sabitov, I. Kh.
Shardurov, V. V.
Konyushkov, A. A.
Gakhov, F. D.
Il’in, V. A.
Nakhyshev, A. M.
Chirka, E. M.
Lykashenko, T. P.
Krushkal’, S. L.
Lumiste, Ü.
Toponogov, V. A.
Burago, Yu. D.
Aleksandrov, A. D.
Berestovskiĭ, V. N.
Tikhomirov, V. M.
Lukashenko, T. P.
Emel’yanov, V. F.
Rudyak, Yu. B.
Kopytov, V. M.
Parshin, A. N.
Bakhturin, Yu. A.
and
Zhevlakov, K. A.
1995.
Encyclopaedia of Mathematics.
p.
715.
Grumbach, Stéphane
and
Su, Jianwen
1997.
Finitely Representable Databases.
Journal of Computer and System Sciences,
Vol. 55,
Issue. 2,
p.
273.
Vorobyov, S.
1997.
The "Hardest" natural decidable theory.
p.
294.
Hintikka, Jaakko
and
Sandu, Gabriel
1997.
Handbook of Logic and Language.
p.
361.
Harizanov, Valentina S.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
3.
Ershov, Y.L.
Goncharov, S.S.
Nerode, A.
and
Remmel, J.B.
1998.
Handbook of Recursive Mathematics - Volume 2: Recursive Algebra, Analysis and Combinatorics.
Vol. 139,
Issue. ,
p.
vii.
Morozov, A.S.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
311.
Ershov, Y.L.
Goncharov, S.S.
Nerode, A.
and
Remmel, J.B.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
vii.
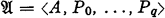 where A is a non-empty set and each Pk is a relation among the elements of A, having the same number of places as Pk.
where A is a non-empty set and each Pk is a relation among the elements of A, having the same number of places as Pk.

