Article contents
SCOTT COMPLEXITY OF COUNTABLE STRUCTURES
Published online by Cambridge University Press: 01 February 2021
Abstract
We define the Scott complexity of a countable structure to be the least complexity of a Scott sentence for that structure. This is a finer notion of complexity than Scott rank: it distinguishes between whether the simplest Scott sentence is 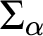 $\Sigma _{\alpha }$
,
$\Sigma _{\alpha }$
, 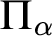 $\Pi _{\alpha }$
, or
$\Pi _{\alpha }$
, or 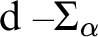 $\mathrm {d-}\Sigma _{\alpha }$
. We give a complete classification of the possible Scott complexities, including an example of a structure whose simplest Scott sentence is
$\mathrm {d-}\Sigma _{\alpha }$
. We give a complete classification of the possible Scott complexities, including an example of a structure whose simplest Scott sentence is 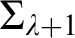 $\Sigma _{\lambda + 1}$
for
$\Sigma _{\lambda + 1}$
for 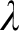 $\lambda $
a limit ordinal. This answers a question left open by A. Miller.
$\lambda $
a limit ordinal. This answers a question left open by A. Miller.
We also construct examples of computable structures of high Scott rank with Scott complexities 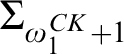 $\Sigma _{\omega _1^{CK}+1}$
and
$\Sigma _{\omega _1^{CK}+1}$
and 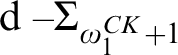 $\mathrm {d-}\Sigma _{\omega _1^{CK}+1}$
. There are three other possible Scott complexities for a computable structure of high Scott rank:
$\mathrm {d-}\Sigma _{\omega _1^{CK}+1}$
. There are three other possible Scott complexities for a computable structure of high Scott rank: 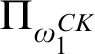 $\Pi _{\omega _1^{CK}}$
,
$\Pi _{\omega _1^{CK}}$
, 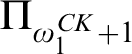 $\Pi _{\omega _1^{CK}+1}$
,
$\Pi _{\omega _1^{CK}+1}$
, 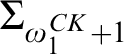 $\Sigma _{\omega _1^{CK}+1}$
. Examples of these were already known. Our examples are computable structures of Scott rank
$\Sigma _{\omega _1^{CK}+1}$
. Examples of these were already known. Our examples are computable structures of Scott rank 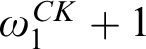 $\omega _1^{CK}+1$
which, after naming finitely many constants, have Scott rank
$\omega _1^{CK}+1$
which, after naming finitely many constants, have Scott rank 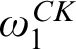 $\omega _1^{CK}$
. The existence of such structures was an open question.
$\omega _1^{CK}$
. The existence of such structures was an open question.
MSC classification
- Type
- Article
- Information
- Copyright
- © Association for Symbolic Logic 2021
References
- 4
- Cited by



