Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T06:19:14.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on identity and description in first-order axiom systems

Published online by Cambridge University Press:  12 March 2014

Theodore Hailperin
Theodore Hailperin*
Affiliation:
Lehigh University
Get access Rights & Permissions [Opens in a new window]

Extract

Hilbert and Ackermann ([1], p. 107) define a first order axiom system as one in which the axioms contain one or more predicate constants, but no predicate variables. Here “axiom” refers to the specific subject-matter axioms and not to the rules of the restricted predicate calculus (quantification theory), which rules are presupposed for each first-order system. It is pointed out by them that an exception could be made for the predicate of identity; for the axiom scheme for this predicate, namely

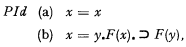
which has in (b) the variable predicate F, could nevertheless be replaced, in any given first-order system, by a finite set of axioms without predicate variables. Thus, for example, if Φ[x, y) is the one constant predicate of such a system then PId(b) could be replaced by

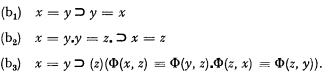
Thus one postulates, in addition to the reflexivity, symmetry, and transitivity of identity, the substitutivity of identical entities in each of the possible “atomic” contexts of a variable (occurrences in the primitive predicates). In this method of introducing identity it has to be taken as an additional primitive predicate and further axioms are consequently needed. In such a system having PId(a), (b1)−(b3) as axioms, the scheme PId(b) can be derived as a meta-theorem of the system, F(x) then being any formula of the system.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 19 , Issue 1 , March 1954 , pp. 14 - 20
Copyright
Copyright © Association for Symbolic Logic 1954

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

[1]Hilbert, D. and Ackermann, W., Principles of mathematical logic, (Chelsea Publishing Co.), New York, 1950.Google Scholar
[2]Robinson, Abraham, On the independence of the axioms of definiteness (Axiome der Bestimmtheit), this Journal, vol. 4 (1939), pp. 69–72.Google Scholar
[3]Hilbert, D. and Bernays, P., Grundlagen der Mathematik, Erster Band, (Springer), Berlin, 1934.Google Scholar
[4]Rosser, J. B., On the consistency of Quine's new foundations for mathematical logic, this Journal, vol. 4 (1939), pp. 15–24.Google Scholar
[5]Rosser, J. B., Logic for mathematicians, (McGraw-Hill), New York, 1953.Google Scholar
[6]Russell, Bertrand, On denoting. Mind, n.s. vol. 14 (1905), pp. 479–493.CrossRefGoogle Scholar
[7]Quine, W. V., Methods of logic, (Henry Holt), New York, 1950.Google Scholar
[8]Gödel, Kurt, Die Vollständigkeit der Axiome des logischen Funktionenkalküls, Monatshefte für Mathematik und Physik, vol. 37 (1930), pp. 349–360.CrossRefGoogle Scholar