No CrossRef data available.
Article contents
A remark on Scott's interpolation theorem for Lω1ω
Published online by Cambridge University Press: 12 March 2014
Extract
In [1], H. Africk proved that Scott's interpolation theorem does not hold in the infinitary logic Lω1ω. In this paper we shall show that there is an interpolation theorem in Lω1ω which can be considered as an extension of Scott's interpolation theorem in Lω1ω by using a technique developed in Motohashi [2] and [3]. We use the terminology in [1]. Therefore {Ri; i ∈ J} is the set of predicate symbols in our language. Now let us divide the set of all the free variables into mutually disjoint infinite sets {VI; I ⊆ J}. Suppose that ℱ ⊆ 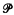 (J). Then a formula in Lω1ω is said to be an ℱ′-formula if it is obtained from atomic formula of the form Ri(X1, …, Xn) for some I ∈ i ∈ I and X1, …, Xn in V1,, by applying ¬ (negation), ∧ (countable conjunction), ∨ (countable disjunction), → (implication), ∀ (universal quantification), and ∃ (existential quantification). Notice that every ℱ-sentence in [1] is an ℱ′. sentence (ℱ′-closed formula) in our sense.
(J). Then a formula in Lω1ω is said to be an ℱ′-formula if it is obtained from atomic formula of the form Ri(X1, …, Xn) for some I ∈ i ∈ I and X1, …, Xn in V1,, by applying ¬ (negation), ∧ (countable conjunction), ∨ (countable disjunction), → (implication), ∀ (universal quantification), and ∃ (existential quantification). Notice that every ℱ-sentence in [1] is an ℱ′. sentence (ℱ′-closed formula) in our sense.
Then we have the following theorem which is an immediate consequence of the interpolation theorem in [2].
Theorem. Let A and ? be sentences. There is an ℱ′-sentence C such that A→C and C→B are provable iff whenever 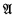 and
and 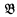 are ℱ-isomorphic structures and
are ℱ-isomorphic structures and 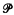 satisfies A, then
satisfies A, then 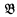 satisfies B.
satisfies B.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1977


