Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T10:35:13.612Z Has data issue: false hasContentIssue false
  • English
  • Français

Relativised quantification: Some canonical varieties of sequence-set algebras

Published online by Cambridge University Press:  12 March 2014

Hajnal Andréka ,
Robert Goldblatt  and
István Németi
Hajnal Andréka
Affiliation:
Mathematical Institute of The Hungarian Academy of Sciences, P. O. Box 127, H-1364 Budapest, Hungary, E-mail: [email protected]
Robert Goldblatt
Affiliation:
School of Mathematical and Computing Sciences, Victoria University, P. O. Box 600, Wellington, New Zealand, E-mail: [email protected]
István Németi
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, P. O. Box 127, H-1364 Budapest, Hungary, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

This paper explores algebraic aspects of two modifications of the usual account of first-order quantifiers.

Standard first-order quantificational logic is modelled algebraically by cylindric algebras. Prime examples of these are algebras whose members are sets of sequences: given a first-order model U for a language that is based on the set {υκ: κ < α} of variables, each formula φ is represented by the set

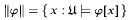
of all those α-length sequences x = 〈xκ: κ < α〉 that satisfy φ in U. Such a sequence provides a value-assignment to the variables (υκ is assigned value xκ), but it may also be viewed geometrically as a point in the α-dimensional Cartesian spaceαU of all α-length sequences whose terms come from the underlying set U of U. Then existential quantification is represented by the operation of cylindrification. To explain this, define a binary relation Tκ on sequences by putting xTκy if and only if x and y differ at most at their κth coordinate, i.e.,

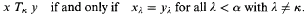
Then for any set X ⊆ αU, the set

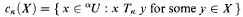
is the “cylinder” generated by translation of X parallel to the κth coordinate axis in αU. Given the standard semantics for the existential quantifier ∃υκ as

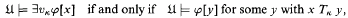
it is evident that

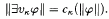
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 1 , March 1998 , pp. 163 - 184
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alechina, N. and van Lambalgen, M., Correspondence and completeness for generalised quantifiers, Technical Report X-94-03, Institute for Logic, Language and Computation (ILLC), University of Amsterdam, 1994.Google Scholar
[2]Alechina, Natasha, Modal quantifiers, Ph.D. thesis, University of Amsterdam, 1995.Google Scholar
[3]Andréka, H., A finite equational axiomatization of Gn, manuscript, Mathematical Institute, Budapest, 09 1995.Google Scholar
[4]Andréka, H. and Thomson, R. J., A Stone type representation theorem for algebras of relations of higher rank, Transactions of the American Mathematical Society, vol. 309 (1988), pp. 671–682.Google Scholar
[5]Andréka, H., van Benthem, J., and Németi, I., Modal languages and bounded fragments of predicate logic, to appear in Journal of Philosophical Logic, 1996.Google Scholar
[6]Goldblatt, Robert, Varieties of complex algebras, Annals of Pure and Applied Logic, vol. 44 (1989), pp. 173–242.CrossRefGoogle Scholar
[7]Goldblatt, Robert, Elementary generation and canonicity for varieties of Boolean algebras with operators, Algebra Universalis, vol. 34 (1995), pp. 551–607.CrossRefGoogle Scholar
[8]Goldblatt, Robert, Algebraic polymodal logic, Research Report 96–175, Mathematics Department, Victoria University of Wellington, to appear in Handbook of Algebraic Logic (Andréka, H.et. al., editors), Kluwer Academic Publishers, in preparation, 01 1996.Google Scholar
[9]Henkin, L., Monk, J. D., and Tarski, A., Cylindric algebras I, North-Holland, 1971.Google Scholar
[10]Henkin, L., Monk, J. D., and Tarski, A., Cylindric algebras II, North-Holland, 1985.Google Scholar
[11]Henkin, L., Monk, J. D., Tarski, A., Andréka, H., and Németi, I., Cylindric set algebras I, Lecture Notes in Mathematics, no. 883, Springer-Verlag, 1981.CrossRefGoogle Scholar
[12]Jónsson, B. and Tarski, A., Boolean algebras with operators, Part I, American Journal of Mathematics, vol. 73 (1951), pp. 891–939.CrossRefGoogle Scholar
[13]Marx, Maarten, Algebraic relativization and arrow logic, Ph.D. thesis, University of Amsterdam, 1995.Google Scholar
[14]Mikulás, Szabolcs, Taming logics, Ph.D. thesis, University of Amsterdam, 1995.Google Scholar
[15]Monk, J. D., Lectures on cylindric set algebras, Algebraic methods in logic and in computer science (Rauzer, C., editor), Banach Center Publications, no. 28, Institute of Mathematics, Polish Academy of Sciences, 1993, pp. 253–290.Google Scholar
[16]Németi, I., Connections between cylindric algebras and initial algebra semantics of CF languages, Mathematical logic in computer science (Dömölki, B. and Gergely, T., editors), Colloquia Mathematica Societatis Jönos Bolyai, vol. 26, North-Holland, 1981, Proceedings of Conference in Salgótarjön, Hungary, 1978, pp. 561–605.Google Scholar
[17]Németi, I., Free algebras and decidability in algebraic logic, technical report, Hungarian Academy of Sciences, Budapest (in Hungarian, Dissertation for D. Sc.), 1986.Google Scholar
[18]Németi, I., Decidable versions of first order logic and cylindric-relativised set algebras, Logic colloquium '92 (Csirmaz, L., Gabbay, D. M., and de, M. Rijke, editors), CSLI Publications, Stanford, California, and European Association for Logic, Language and Information, 1995, pp. 177–241.Google Scholar