Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T11:11:05.737Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular embeddings of the stationary tower and Woodin's 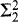maximality theorem

Published online by Cambridge University Press:  12 March 2014

Richard Ketchersid ,
Paul B. Larson  and
Jindřich Zapletal
Richard Ketchersid
Affiliation:
Department of Mathematics, Miami University Oxford, Ohio 45056, USA. E-mail: [email protected]
Paul B. Larson
Affiliation:
Department of Mathematics, Miami University Oxford, Ohio 45056, USA. E-mail: [email protected]
Jindřich Zapletal
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611, USA. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present Woodin's proof that if there exists a measurable Woodin cardinal δ then there is a forcing extension satisfying all 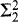sentences ϕ such that CH + ϕ holds in a forcing extension of V by a partial order in Vδ. We also use some of the techniques from this proof to show that if there exists a stationary limit of stationary limits of Woodin cardinals, then in a homogeneous forcing extension there is an elementary embedding j: V → M with critical point 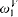such that M is countably closed in the forcing extension.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 2 , June 2010 , pp. 711 - 727
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Farah, I. and Larson, P. B., Absoluteness for universally Baire sets and the uncountable I, Set theory and its applications, Quaderni di Matematica, vol. 17, 2006, pp. 47–92.Google Scholar
[2]Hamkins, J. D. and Woodin, W. H., Small forcing creates neither strong nor Woodin cardinals, Proceedings of the American Mathematical Society, vol. 128 (2000), no. 10, pp. 3025–3029.CrossRefGoogle Scholar
[3]Jech, T., Set theory, Springer-Verlag, Berlin, 2003.Google Scholar
[4]Kanamori, A., The higher infinite. Large cardinals in set theory from their beginnings, 2nd ed., Springer Monographs in Mathematics, 2003.Google Scholar
[5]Kunen, K., Set theory. An introduction to independence proofs, North Holland, 1983.Google Scholar
[6]Larson, P. B., The stationary tower. Notes on a course by W. Hugh Woodin, American Mathematical Society University Lecture Series, vol. 32, 2004.Google Scholar
[7]Larson, P. B. and Shelah, S., The stationary set splitting game. Mathematical Logic Quarterly, vol. 54 (2008), no. 2, pp. 187–193.CrossRefGoogle Scholar
[8]Schindler, R. and Steel, J., The core model induction, book in preparation.Google Scholar