Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T19:04:41.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Refinements of Vaught's normal from theorem

Published online by Cambridge University Press:  12 March 2014

Victor Harnik
Victor Harnik*
Affiliation:
University of Haifa, Mount Carmel, Haifa 31999, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

The central notion of this paper is that of a (conjunctive) game-sentence, i.e., a sentence of the form

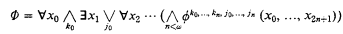
where the indices ki, ji range over given countable sets and the matrix conjuncts are, say, open -formulas. Such game sentences were first considered, independently, by Svenonius [19], Moschovakis [13]—[15] and Vaught [20]. Other references are [1], [3]—[5], [10]—[12]. The following normal form theorem was proved by Vaught (and, in less general forms, by his predecessors).

Theorem 0.1. Let L = L0(R). For every -sentence ϕ there is an L0-game sentence Θ such that ⊨′ ∃Rϕ ↔ Θ.

(A word about the notations: L0(R) denotes the language obtained from L0 by adding to it the sequence R of logical symbols which do not belong to L0; “⊨′α” means that α is true in all countable models.)

0.1 can be restated as follows.

Theorem 0.1′. For every-sentence ϕ there is an L0-game sentence Θ such that ⊨ϕ → Θ and for any-sentence ϕ if ⊨ϕ → ϕ and L′ ⋂ L ⊆ L0, then ⊨ Θ → ϕ.

(We sketch the proof of the equivalence between 0.1 and 0.1′.

0.1 implies 0.1′. This is obvious once we realize that game sentences and their negations satisfy the downward Löwenheim-Skolem theorem and hence, ⊨′α is equivalent to ⊨α whenever α is a boolean combination of and game sentences.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 3 , September 1979 , pp. 289 - 306
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, J., Admissible sets and structures, Perspectives in mathematical logic, Springer, Berlin, 1975.Google Scholar
[2]Craig, W., Linear reasoning. A new form of the Herbrand-Gentzen theorem, this Journal, vol. 22(1957), pp. 250–268.Google Scholar
[3]Harnik, V., Came sentences, recursive saturation and definability, this Journal (to appear).Google Scholar
[4]Harnik, V. and Makkai, M., Applications of Vaught sentences and the covering theorem, this Journal, vol. 41(1976), pp. 171–187.Google Scholar
[5]Harnik, V. and Makkai, M., New axiomatizations for logics with generalized quantifiers, Israel Journal of Mathematics (to appear).Google Scholar
[6]Henkin, L., An extension of the Craig-Lyndon interpolation theorem, this Journal, vol. 28 (1963), pp. 201–216.Google Scholar
[7]Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[8]Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas, Fundamenta Mathematicae, vol. 57(1965), pp. 253–272.CrossRefGoogle Scholar
[9]Lyndon, R., An interpolation theorem in the predicate calculus, Pacific Journal of Mathematics, vol. 9(1959), pp. 129–142.CrossRefGoogle Scholar
[10]Makkai, M., Svenonius sentences and Lindström's theory on preservation theorems, Fundamenta Mathematicae, vol. 73(1971), pp. 219–233.CrossRefGoogle Scholar
[11]Makkai, M., Vaught sentences and Lindström's regular relations, Lecture Notes in Mathematics, no. 337, Cambridge Summer School in Mathematical Logic, Springer, Berlin, 1973, pp. 622–660.Google Scholar
[12]Makkai, M., Admissible sets and infinitary logic, Handbook of Mathematical Logic (Barwise, J., Editor), North-Holland, Amsterdam, 1977, pp. 233–282.CrossRefGoogle Scholar
[13]Moschovakis, Y. N., The Suslin-Kleene theorem for countable structures, Duke Mathematical Journal, vol. 37(1970), pp. 341–352.CrossRefGoogle Scholar
[14]Moschovakis, Y. N., The game quantifier, Proceedings of the American Mathematical Society, vol. 31 (1972), pp. 245–250.CrossRefGoogle Scholar
[15]Moschovakis, Y. N., Elementary induction on abstract structures, North-Holland, Amsterdam, 1974.Google Scholar
[16]Oberschelp, A., On the Craig-Lyndon interpolation theorem, this Journal, vol. 33(1968), pp. 271–274.Google Scholar
[17]Ressayre, J. P., Models with compactness properties relative to an admissible language, Annals of Mathematical Logic, 11 (1977), pp. 31–55.CrossRefGoogle Scholar
[18]Smullyan, R., First order logic, Springer-Verlag, Berlin and New York, 1968.CrossRefGoogle Scholar
[19]Svenonius, L., On the denumerable models of theories with extrapredicates, The theory of models, North-Holland, Amsterdam, 1965, pp. 376–389.Google Scholar
[20]Vaught, R. L., Descriptive set theory in , Lecture Notes in Mathematics, no. 337, Cambridge Summer School of Mathematical Logic, Springer, Berlin, 1973, pp. 574–598.Google Scholar