Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-03T02:28:44.034Z Has data issue: false hasContentIssue false
  • English
  • Français

A reduction in the number of primitive ideas of arithmetic

Published online by Cambridge University Press:  12 March 2014

John R. Myhill
John R. Myhill*
Affiliation:
Temple University
Get access Rights & Permissions [Opens in a new window]

Extract

Let

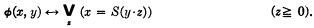
We shall show that every formula in the elementary arithmetic of positive integers may be constructed out of matrices of the form ϕ(x, y) by means of quantifiers and the stroke. For Julia Robinson has shown that the successor function and the relation of divisibility are sufficient to define addition and multiplication; but from elementary considerations

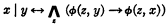
and

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 15 , Issue 2 , June 1950 , pp. 130
Copyright
Copyright © Association for Symbolic Logic 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

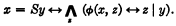
1 Robinson, Julia, Definability and decision problems in arithmetic, this Journal, vol. 14 (1949), pp. 98–114Google Scholar, Theorem 1.1.

2 Julia Robinson, loc. cit., Theorem 1.2.