Article contents
Reduced products and nonstandard logics1
Published online by Cambridge University Press: 12 March 2014
Extract
The results of the present paper were announced in [1]. The work is divided into our parts. In the first part we define relations 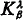 (relations between relational struc tures) and we show their connection with the equivalence of the languages LΚ,λ (Theorem 1). The relations
(relations between relational struc tures) and we show their connection with the equivalence of the languages LΚ,λ (Theorem 1). The relations 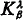 generalize the games Gn (n < ω) of Ehrenfeucht (see [2]) and the conditions (i)–(ii) which were used by Karp in [5].
generalize the games Gn (n < ω) of Ehrenfeucht (see [2]) and the conditions (i)–(ii) which were used by Karp in [5].
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1969
Footnotes
I wish to express my gratitude to Prof. A. Mostowski who greatly encouraged me during the preparation of this paper.
References
- 12
- Cited by


