Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-25T00:35:16.682Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursive functions in basic logic

Published online by Cambridge University Press:  12 March 2014

Frederic B. Fitch
Frederic B. Fitch*
Affiliation:
Yale University
Get access Rights & Permissions [Opens in a new window]

Extract

1.1 The system K* of basic logic, as presented in a previous paper, will be shown to be formalizable in an alternative way according to which the rule [E],

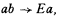
is replaced by the rule [F],

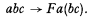
1.2. General recursive functions will be shown to be definable in K* in a way that retains functional notation, so that the equation,

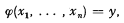
will be formalized in K* by the formula,

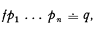
where ‘f’, ‘p1’, … ‘pn’ respectively denote φ, x1, …, xn, and where ‘≐’ plays the role of numerical equality. Partial recursive functions may be handled in a similar way. The rule [E] is not required for dealing with primitive recursive functions by this method.

1.3. An operator ‘G’ will be defined such that ‘[Ga ≐ p]’ is a theorem of K* if and only if ‘p’ denotes the Gödel number of ‘a’.

1.4. In reformulating K* we assume ‘o0’, ‘o1,’ ‘o2’, …, have been so chosen that we can determine effectively whether or not a given U-expression is the mth member of the above series. The revised rules for K* are then as follows. (Double-arrow forms of these rules are derivable, except in the case of rule [V].)

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 21 , Issue 4 , December 1956 , pp. 337 - 346
Copyright
Copyright © Association for Symbolic Logic 1956

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Fitch, F. B., A simplification of basic logic, this Journal, vol. 18 (1953), pp. 317–325Google Scholar. This paper will be referred to as SBL. Closely related to it are my two papers, A definition of negation in extended basic logic, ibid. vol. 19 (1954), pp. 29–36, referred to as DN, and Self-referential relations, Actes du XIème Congrès International de Philosophie, vol. 14, pp. 121–127, Amsterdam, 1953Google Scholar. The above papers are based on my following three earlier papers: A basic logic, this Journal, vol. 7 (1942), pp. 105–114Google Scholar, referred to as BL; Representations of calculi, this Journal, vol. 9 (1944), pp. 57–62Google Scholar, referred to as RC; An extension of basic logic, this Journal, vol. 13 (1948), pp. 95–106Google Scholar.

2 A method not retaining functional notation was given in RC. Some well-known properties of general recursive functions are presupposed in what follows. In connection with the theory of general recursive functions see Kleene, S. C., Introduction to metamathematics, Amsterdam, 1952Google Scholar.