Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-03T18:49:37.180Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursion theory on orderings. II

Published online by Cambridge University Press:  12 March 2014

J. B. Remmel
J. B. Remmel*
Affiliation:
University of California at San Diego, La Jolla, California 92037
Get access Rights & Permissions [Opens in a new window]

Extract

In [6], G. Metakides and the author introduced a general model theoretic setting in which to study the lattice of r.e. substructures of a large class of recursively presented models 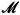. Examples included 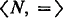, the natural numbers with equality, 〈 Q, ≤ 〉, the rationals under the usual ordering, and a large class of n-dimensional partial orderings. In this setting, we were able to generalize many of the constructions of classical recursion theory so that the constructions yield the classical results when we specialize to the case of 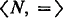and new results when we specialize to other models. Constructions to generalize Myhill's Theorem on creative sets [8], Friedberg's Theorem on the existence of maximal sets [3], Dekker's Theorem on the degrees of hypersimple sets [2], and Martin's Theorem on the degrees of maximal sets [5] were produced in [6]. In this paper, we give constructions to generalize the Morley-Soare Splitting Theorem [7] and Lachlan's characterization of hyperhypersimple sets [4] in §2, constructions to generalize Lachlan's theorems on the existence of major subsets and r-maximal sets contained in maximal sets [4] in §3, and constructions to generalize Robinson's construction of r-maximal sets that are not contained in any maximal sets [11] and second-order maximal sets [12] in §4.

In §1 of this paper, we give the precise definitions of our model theoretic setting and deal with other preliminaries. Also in §1, we define the notions of “uniformly nonrecursive”, “uniformly maximal”, etc. which are the key notions involved in the generalizations of the various theorems that occur in §§2, 3 and 4.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 45 , Issue 2 , June 1980 , pp. 317 - 333
Copyright
Copyright © Association for Symbolic Logic 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cooper, S. B., Jump equivalence of the Δ20 hyperhyperimmune sets, this Journal, vol. 37 (1972), pp. 598–600.Google Scholar
[2]Dekker, J. C. E., A theorem on hypersimple sets, Proceedings of the American Mathematical Society, vol. 5 (1954), pp. 791–796.CrossRefGoogle Scholar
[3]Friedberg, R. M., Three theorems on recursive enumeration. I. Decomposition. II. Maximal sets. III. Enumeration without duplication, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[4]Lachlan, A. H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
[5]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
[6]Metakides, G. and Remmel, J. B., Recursion theory on orderings. I. A model theoretic setting, this Journal vol. 44 (1979), pp. 383–402.Google Scholar
[7]Morley, M. D. and Soare, R., Boolean algebras, splitting theorems, and Δ20 sets, Fundamenta Mathematicae, vol. 90 (1975), pp. 45–51.CrossRefGoogle Scholar
[8]Myhill, J., Creative sets, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 97–108.CrossRefGoogle Scholar
[9]Owings, J. C., Recursion, metarecursion and inclusion, this Journal, vol. 32 (1967), pp. 173–178.Google Scholar
[10]Post, E. L., Recursively enumerable sets of positive integers and their decision problems, Bulletin of the American Mathematical Society, vol. 50 (1944), pp. 284–316.CrossRefGoogle Scholar
[11]Robinson, R. W., Simplicity of recursively emunerable sets, this Journal, vol. 32 (1967), pp. 162–172.Google Scholar
[12]Robinson, R. W., Two theorems on hyperhypersimple sets, Transactions of the American Mathematical Society, vol. 128 (1967), pp. 531–538.CrossRefGoogle Scholar
[13]Rogers, H. J. Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[14]Sacks, G. E., Degrees of unsolvability (revised edition). Annals of Mathematical Studies, no. 55, Princeton University Press, Princeton, NJ, 1966.Google Scholar