Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-03T02:11:04.278Z Has data issue: false hasContentIssue false
  • English
  • Français

REASONING FROM HYPOTHESES IN $\ast $-CONTINUOUS ACTION LATTICES

Part of: Proof theory and constructive mathematics General logic Computability and recursion theory

Published online by Cambridge University Press:  26 February 2025

STEPAN L. KUZNETSOV Open the ORCID record for STEPAN L. KUZNETSOV [Opens in a new window] ,
TIKHON PSHENITSYN Open the ORCID record for TIKHON PSHENITSYN [Opens in a new window]  and
STANISLAV O. SPERANSKI Open the ORCID record for STANISLAV O. SPERANSKI [Opens in a new window]
STEPAN L. KUZNETSOV*
Affiliation:
DEPARTMENT OF MATHEMATICAL LOGIC STEKLOV MATHEMATICAL INSTITUTE OF RUSSIAN ACADEMY OF SCIENCES MOSCOW, RUSSIA E-mail: [email protected] E-mail: [email protected]
TIKHON PSHENITSYN
Affiliation:
DEPARTMENT OF MATHEMATICAL LOGIC STEKLOV MATHEMATICAL INSTITUTE OF RUSSIAN ACADEMY OF SCIENCES MOSCOW, RUSSIA E-mail: [email protected] E-mail: [email protected]
STANISLAV O. SPERANSKI
Affiliation:
DEPARTMENT OF MATHEMATICAL LOGIC STEKLOV MATHEMATICAL INSTITUTE OF RUSSIAN ACADEMY OF SCIENCES MOSCOW, RUSSIA E-mail: [email protected] E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The class of all $\ast $-continuous Kleene algebras, whose description includes an infinitary condition on the iteration operator, plays an important role in computer science. The complexity of reasoning in such algebras—ranging from the equational theory to the Horn one, with restricted fragments of the latter in between—was analyzed by Kozen (2002). This paper deals with similar problems for $\ast $-continuous residuated Kleene lattices, also called $\ast $-continuous action lattices, where the product operation is augmented by residuals. We prove that, in the presence of residuals, the fragment of the corresponding Horn theory with $\ast $-free hypotheses has the same complexity as the 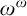$\omega ^\omega $ iteration of the halting problem, and hence is properly hyperarithmetical. We also prove that if only commutativity conditions are allowed as hypotheses, then the complexity drops down to 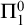$\Pi ^0_1$ (i.e., the complement of the halting problem), which is the same as that for $\ast $-continuous Kleene algebras. In fact, we get stronger upper bound results: the fragments under consideration are translated into suitable fragments of infinitary action logic with exponentiation, and our upper bounds are obtained for the latter ones.

Keywords

Kleene algebraaction latticeinfinitary action logicexponentiationcomplexityhyperarithmetical hierarchy

MSC classification

Primary: 03B47: Substructural logics (including relevance, entailment, linear logic, Lambek calculus, BCK and BCI logics) 03D35: Undecidability and degrees of sets of sentences
Secondary: 03B70: Logic in computer science 03F07: Structure of proofs 03F52: Linear logic and other substructural logics
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 39
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aczel, P., An introduction to inductive definitions , Handbook of Mathematical Logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 739–782.Google Scholar
Azevedo de Amorim, A., Zhang, C., and Gaboardi, M., Kleene algebra with commutativity conditions is undecidable , 33rd EACSL Annual Conference on Computer Science Logic (CSL 2025) (Endrullis, J. and Schmitz, S., editors), Leibniz International Proceedings in Informatics (LIPIcs), 326, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, 2025, pp. 36:1–36:25.Google Scholar
Andreoli, J.-M., Logic programming with focusing proofs in linear logic . Journal of Logic and Computation , vol. 2 (1992), no. 3, pp. 297–347.Google Scholar
Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy , North-Holland, Amsterdam, 2000.Google Scholar
Book, R. V. and Otto, F., String-Rewriting Systems , Springer, New York, 1993.Google Scholar
Buchholz, W., Explaining Gentzen’s consistency proof within infinitary proof theory , Computational Logic and Proof Theory, KGC ’97 (Gottlob, G., Leitsch, A., and Mundici, D., editors), Lecture Notes in Computer Science, 1289, Springer, Berlin, Heidelberg, 1997, pp. 4–17.Google Scholar
Buszkowski, W., On action logic: Equational theories of action algebras . Journal of Logic and Computation , vol. 17 (2007), no. 1, pp. 199–217.Google Scholar
Galatos, N., Jipsen, P., Kowalski, T., and Ono, H., Residuated Lattices: An Algebraic Glimpse at Substructural Logics , Studies in Logic and the Foundations of Mathematics, 151, Elsevier, Amsterdam, 2007.Google Scholar
Girard, J.-Y., Linear logic . Theoretical Computer Science , vol. 50 (1987), no. 1, pp. 1–101.Google Scholar
Kanovich, M., Kuznetsov, S., Nigam, V., and Scedrov, A., Subexponentials in non-commutative linear logic . Mathematical Structures in Computer Science , vol. 29 (2019), no. 8, pp. 1217–1249.Google Scholar
Kleene, S. C., Representation of events in nerve nets and finite automata , Automata Studies (Shannon, C. E. and McCarthy, J., editors), Princeton University Press, Princeton, NJ, 1956, pp. 3–41.Google Scholar
Kozen, D., A completeness theorem for Kleene algebras and the algebra of regular events . Information and Computation , vol. 110 (1994), no. 2, pp. 366–390.Google Scholar
Kozen, D., On action algebras , Logic and Information Flow (Eijck, J. van and Visser, A., editors), MIT Press, Cambridge, MA, 1994, pp. 78–88.Google Scholar
Kozen, D., On the complexity of reasoning in Kleene algebra . Information and Computation , vol. 179 (2002), pp. 152–162.Google Scholar
Krull, W., Axiomatische Begründung der allgemeinen Idealtheorie . Sitzungsberichte der physikalischmedizinischen Sozietät zu Erlangen , vol. 56 (1924), pp. 47–63.Google Scholar
Kuznetsov, S. L., A ${\varPi}_1^0$ -bounded fragment of infinitary action logic with exponential, Logic, Language, and Security. Essays Dedicated to Andre Scedrov on the Occasion of his 65th Birthday (V. Nigam et al., editors), Lecture Notes in Computer Science, 12300, Springer, Cham, 2020, pp. 3–16.Google Scholar
Kuznetsov, S. L., Action logic is undecidable . ACM Transactions on Computational Logic , vol. 22 (2021), no. 2, 10.Google Scholar
Kuznetsov, S. L., Complexity of a fragment of infinitary action logic with exponential via non-well-founded proofs , Automated Reasoning with Analytic Tableaux and Related Methods — TABLEAUX 2021 (Das, A. and Negri, S., editors), Lecture Notes in Computer Science, 12842, Springer, Cham, 2021, pp. 317–334.Google Scholar
Kuznetsov, S. L., On the complexity of reasoning in Kleene algebra with commutativity conditions , Theoretical Aspects of Computing — ICTAC 2023 (Ábrahám, E., Dubslaff, C., and Tarifa, S. L. T., editors), Lecture Notes in Computer Science, 14446, Springer, Cham, 2023, pp. 83–99.Google Scholar
Kuznetsov, S. L., Algorithmic complexity for theories of commutative Kleene algebras . Izvestiya: Mathematics , vol. 88 (2024), no. 2, pp. 236–269.Google Scholar
Kuznetsov, S. L. and Speranski, S. O., Infinitary action logic with exponentiation . Annals of Pure and Applied Logic , vol. 173 (2022), no. 2, 103057.Google Scholar
Kuznetsov, S. L. and Speranski, S. O., Infinitary action logic with multiplexing , Studia Logica , vol. 111 (2023), no. 2, pp. 251–280.Google Scholar
Lambek, J., The mathematics of sentence structure . American Mathematical Monthly , vol. 65 (1958), pp. 154–170.Google Scholar
Montalbán, A., Computable Structure Theory: Beyond the Arithmetic, Draft of the Book, 2022.Google Scholar
Moschovakis, Y. N., Elementary Induction on Abstract Structures , North-Holland, Amsterdam, 1974.Google Scholar
Palka, E., An infinitary sequent system for the equational theory of *-continuous action lattices . Fundamenta Informaticae , vol. 78 (2007), no. 2, pp. 295–309.Google Scholar
Pohlers, W., Proof Theory: An Introduction , Lecture Notes in Mathematics, 1407, Springer, Berlin, Heidelberg, 1989.Google Scholar
Pratt, V., Action logic and pure induction , Logics in AI — JELIA 1990 (Eijck, J. van, editor), Lecture Notes in Artificial Intelligence, 478, Springer, Berlin, Heidelberg, 1990, pp. 97–120.Google Scholar
Pshenitsyn, T., Closure ordinal of immediate derivability operator of infinitary action logic . Mathematical Notes , vol. 116 (2024), no. 4, pp. 729–744.Google Scholar
Pshenitsyn, T., Hyperarithmetical complexity of infinitary action logic with multiplexing . Logic Journal of the IGPL , vol. 33 (2025), no. 2, article number jzae078.Google Scholar
Rogers, H. Jr., Theory of Recursive Functions and Effective Computability , McGraw-Hill Book Company, New York, 1967.Google Scholar
Ward, M. and Dilworth, R. P., Residuated lattices . Transactions of the AMS , vol. 45 (1939), no. 3, pp. 335–354.Google Scholar