Article contents
Reals n-generic relative to some perfect tree
Published online by Cambridge University Press: 12 March 2014
Abstract
We say that a real X is n-generic relative to a perfect tree T if X is a path through T and for all 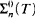 sets S, there exists a number k such that either X∣k ϵ S or for all a σ ϵ T extending X∣k we have a σ ∉ S. A real X is n-generic relative to some perfect tree if there exists such a T. We first show that for every number n all but countably many reals are n-generic relative to some perfect tree. Second, we show that proving this statement requires ZFC− + “∃ infinitely many iterates of the power set of ω”. Third, we prove that every finite iterate of the hyperjump,
sets S, there exists a number k such that either X∣k ϵ S or for all a σ ϵ T extending X∣k we have a σ ∉ S. A real X is n-generic relative to some perfect tree if there exists such a T. We first show that for every number n all but countably many reals are n-generic relative to some perfect tree. Second, we show that proving this statement requires ZFC− + “∃ infinitely many iterates of the power set of ω”. Third, we prove that every finite iterate of the hyperjump, 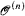 , is not 2-generic relative to any perfect tree and for every ordinal α below the least λ such that supβ<λ (βth admissible) = λ, the iterated hyperjump
, is not 2-generic relative to any perfect tree and for every ordinal α below the least λ such that supβ<λ (βth admissible) = λ, the iterated hyperjump 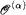 is not 5-generic relative to any perfect tree. Finally, we demonstrate some necessary conditions for reals to be 1-generic relative to some perfect tree.
is not 5-generic relative to any perfect tree. Finally, we demonstrate some necessary conditions for reals to be 1-generic relative to some perfect tree.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 1
- Cited by


