Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T18:02:04.470Z Has data issue: false hasContentIssue false
  • English
  • Français

Random reals, the rainbow Ramsey theorem, and arithmetic conservation

Published online by Cambridge University Press:  12 March 2014

Chris J. Conidis  and
Theodore A. Slaman
Chris J. Conidis
Affiliation:
Department of Mathematics, 200, University Ave. West, University of Waterloo, Waterloo, ON N2L 3G1, Canada, E-mail: [email protected]
Theodore A. Slaman
Affiliation:
Department of Mathematics, University of California, Berkeley, Berkeley, CA 94720-3840, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the question “To what extent can random reals be used as a tool to establish number theoretic facts?” Let 2-RAN be the principle that for every real X there is a real R which is 2-random relative to X. In Section 2, we observe that the arguments of Csima and Mileti [3] can be implemented in the base theory RCA0 and so RCA0 + 2-RAN implies the Rainbow Ramsey Theorem. In Section 3, we show that the Rainbow Ramsey Theorem is not conservative over RCA0 for arithmetic sentences. Thus, from the Csima–Mileti fact that the existence of random reals has infinitary-combinatorial consequences we can conclude that 2-RAN has non-trivial arithmetic consequences. In Section 4, we show that 2-RAN is conservative over RCA0 + BΣ2 for 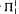-sentences. Thus, the set of first-order consequences of 2-RAN is strictly stronger than P− + IΣ1 and no stronger than P− + BΣ2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 1 , March 2013 , pp. 195 - 206
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cholak, Peter A., Jockusch, Carl G., and Slaman, Theodore A., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[2]Cholak, Peter A., Jockusch, Carl G., and Slaman, Theodore A., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[3]Csima, Barbara F. and Mileti, Joseph R., The strength of the rainbow Ramsey theorem, this Journal, vol. 74 (2009), no. 4, pp. 1310–1324.Google Scholar
[4]Downey, R. G. and Hirschfeldt, D., Algorithmic randomness and complexity, Theory and Applications of Computability, Springer, 2010.CrossRefGoogle Scholar
[5]Hájek, P. and Pudlák, P., Metamathematics of first-order arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998, second printing.Google Scholar
[6]Hirst, J. L., Combinatorics in subsystems of second order arithmetic, Ph.D. thesis, The Pennsylvania State University, 1987.Google Scholar
[7]Jocksuch, Carl G., Ramsey's theorem and recursion theory, this Journal, vol. 37 (1972), no. 2, pp. 268–280.Google Scholar
[8]Kaye, Richard, Models of Peano arithmetic, Oxford Logic Guides, vol. 15, The Clarendon Press Oxford University Press, 1991.CrossRefGoogle Scholar
[9]Kaye, Richard, The theory of κ-like models of arithmetic, Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 547–559.CrossRefGoogle Scholar
[10]Kaye, Richard, Constructing κ-like models of arithmetic, Journal of the London Mathematical Society. Series 2, vol. 55 (1997), no. 1, pp. 1–10.CrossRefGoogle Scholar
[11]Kirby, L. A. S. and Paris, J. B., Initial segments of models of Peano's axioms, Set theory and hierarchy theory, V (Proceedings of the third conference, Bierutowice, 1976), Lecture Notes in Mathematics, vol. 619, Springer, Berlin, 1977, pp. 221–226.Google Scholar
[12]Martin-Löf, Per, The definition of random sequences, Information and Control, vol. 9 (1966), pp. 602–619.CrossRefGoogle Scholar
[13]Nies, André, Computability and randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
[14]Seetapun, David and Slaman, Theodore A., On the strength of Ramsey's theorem, Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582, Special Issue: Models of arithmetic.CrossRefGoogle Scholar
[15]Simpson, Stephen G., Subsystems of second order arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
[16]Soare, Robert I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.CrossRefGoogle Scholar