Article contents
Ramsey-like cardinals II
Published online by Cambridge University Press: 12 March 2014
Abstract
This paper continues the study of the Ramsey-like large cardinals introduced in [5] and [14]. Ramsey-like cardinals are defined by generalizing the characterization of Ramsey cardinals via the existence of elementary embeddings. Ultrafilters derived from such embeddings are fully iterable and so it is natural to ask about large cardinal notions asserting the existence of ultrafilters allowing only α-many iterations for some countable ordinal α. Here we study such α-iterable cardinals. We show that the α-iterable cardinals form a strict hierarchy for α ≤ ω1, that they are downward absolute to L for 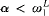 , and that the consistency strength of Schindler's remarkable cardinals is strictly between 1-iterable and 2-iterable cardinals.
, and that the consistency strength of Schindler's remarkable cardinals is strictly between 1-iterable and 2-iterable cardinals.
We show that the strongly Ramsey and super Ramsey cardinals from [5] are downward absolute to the core model K. Finally, we use a forcing argument from a strongly Ramsey cardinal to separate the notions of Ramsey and virtually Ramsey cardinals. These were introduced in [14] as an upper bound on the consistency strength of the Intermediate Chang's Conjecture.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011
References
REFERENCES
- 15
- Cited by


