Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T07:14:01.380Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasi-subtractive varieties

Published online by Cambridge University Press:  12 March 2014

Tomasz Kowalski ,
Francesco Paoli  and
Matthew Spinks
Tomasz Kowalski
Affiliation:
Department of Mathematics and Statistics, University of Melbourne, Melbourne, Australia, E-mail: [email protected]
Francesco Paoli
Affiliation:
Department of Education, University of Cagliari, Cagliari, Italy, E-mail: [email protected]
Matthew Spinks
Affiliation:
Department of Education, University of Cagliari, Cagliari, Italy, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Varieties like groups, rings, or Boolean algebras have the property that, in any of their members, the lattice of congruences is isomorphic to a lattice of more manageable objects, for example normal subgroups of groups, two-sided ideals of rings, filters (or ideals) of Boolean algebras. Abstract algebraic logic can explain these phenomena at a rather satisfactory level of generality: in every member A of a τ-regular variety 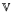the lattice of congruences of A is isomorphic to the lattice of deductive filters on A of the τ-assertional logic of 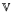. Moreover, if 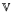has a constant 1 in its type and is 1-subtractive, the deductive filters on A ∈ 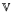of the 1-assertional logic of 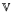coincide with the 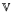-ideals of A in the sense of Gumm and Ursini, for which we have a manageable concept of ideal generation.

However, there are isomorphism theorems, for example, in the theories of residuated lattices, pseudointerior algebras and quasi-MV algebras that cannot be subsumed by these general results. The aim of the present paper is to appropriately generalise the concepts of subtractivity and τ-regularity in such a way as to shed some light on the deep reason behind such theorems. The tools and concepts we develop hereby provide a common umbrella for the algebraic investigation of several families of logics, including substructural logics, modal logics, quantum logics, and logics of constructive mathematics.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 4 , December 2011 , pp. 1261 - 1286
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Aglianò, P. and Ursini, A., On subtractive varieties II: General properties, Algebra Universalis, vol. 36 (1996), pp. 222–259.CrossRefGoogle Scholar
[2]Aglianò, P. and Ursini, A., On subtractive varieties III: From ideals to congruences, Algebra Universalis, vol. 37 (1997), pp. 296–333.CrossRefGoogle Scholar
[3]Aglianò, P. and Ursini, A., On subtractive varieties IV: Definability of principal ideals, Algebra Universalis, vol. 38 (1997), pp. 355–389.CrossRefGoogle Scholar
[4]Ardeshir, M. and Ruitenburg, W., Basic propositional calculus I, Mathematical Logic Quarterly, vol. 44 (1998), pp. 317–343.CrossRefGoogle Scholar
[5]Barbour, G. D. and Raftery, J. G., Quasivarieties of logic, regularity conditions and parameterized algebraization, Studio Logica, vol. 74 (2003), pp. 99–152.CrossRefGoogle Scholar
[6]Blok, W. J. and Pigozzi, D., Algebraizable logics, Memoirs of the AMS, no. 396, American Mathematical Society, Providence, RI, 1989.CrossRefGoogle Scholar
[7]Blok, W. J. and Pigozzi, D., On the structure of varieties with equationally definable principal congruences IV, Algebra Universalis, vol. 31 (1994), pp. 1–35.CrossRefGoogle Scholar
[8]Blok, W. J. and Raftery, J. G., Ideals in quasivarieties of algebras, Models, algebras and proofs (Caicedo, X. and Montenegro, C. H., editors), Leecture Notes in Pure and Applied Mathematics, Dekker, 1999. pp. 167–186.Google Scholar
[9]Blok, W. J. and Raftery, J. G., Assertionally equivalent quasivarieties, International Journal of Algebra and Computation, vol. 18 (2008), pp. 589–681.CrossRefGoogle Scholar
[10]Bou, F., Paoli, F., Ledda, A., and Freytes, H., On some properties of quasi-MV algebras and quasi-MV algebras. Part II, Soft Computing, vol. 12 (2008), pp. 341–352.CrossRefGoogle Scholar
[11]Burris, S. and Sankappanavar, H. P., A course in universal algebra, Graduate Texts in Mathematics, no. 78, Springer, 1981.CrossRefGoogle Scholar
[12]Chajda, I., Congruence properties of algebras in nilpotent shifts of varieties, General algebra and discrete mathematics (Denecke, K. and Lüders, O., editors), Heidermann, Berlin, 1995, pp. 35–46.Google Scholar
[13]Chajda, I., Normally presented varieties, Algebra Universalis, vol. 34 (1995), pp. 327–335.CrossRefGoogle Scholar
[14]Chajda, I., Halas, R., Kühr, J., and Vanzurova, A., Normalization of MV algebras, Mathematica Bohemica, vol. 130 (2005), no. 3, pp. 283–300.CrossRefGoogle Scholar
[15]Czelakowski, J., Equivalential logics I, Studia Logica, vol. 45 (1981), pp. 227–236.CrossRefGoogle Scholar
[16]Darnel, M. R., Theory of lattice ordered groups, Dekker, New York, 1995.Google Scholar
[17]Duda, J., Arithmelicity at 0, Czechoslovak Mathematical Journal, vol. 37 (1987), pp. 197–206.CrossRefGoogle Scholar
[18]Epstein, G. and Horn, A., Logics which are characterised by subresiduated lattices, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 22 (1976), pp. 199–210.CrossRefGoogle Scholar
[19]Font, J. M., Jansana, R., and Pigozzi, D., A survey of abstract algebraic logic, Studia Logica, vol. 74 (2003), pp. 13–97.CrossRefGoogle Scholar
[20]Galatos, N., Jipsen, P., Kowalski, T., and Ono, H., Residuated lattices: An algebraic glimpse on substructurai logics, Logic and the Foundations of Mathematics, vol. 151, Elsevier, Amsterdam, 2007.Google Scholar
[21]Galatos, N. and Tsinakis, C., Generalized MV algebras, Journal of Algebra, vol. 283 (2005), no. 1, pp. 254–291.CrossRefGoogle Scholar
[22]Graczynska, E., On normal and regular identities, Algebra Universalis, vol. 27 (1990), pp. 387–397.CrossRefGoogle Scholar
[23]Grätzer, G., Lakser, H., and Płonka, J., Joins and direct products of equational classes, Canadian Mathematical Bulletin, vol. 12 (1969), pp. 741–744.CrossRefGoogle Scholar
[24]Gumm, H. P. and Ursini, A., Ideals in universal algebra, Algebra Universalis, vol. 19 (1984), pp. 45–54.CrossRefGoogle Scholar
[25]Jónsson, B. and Tsinakis, C., Products of classes of residuated structures, Studia Logica, vol. 77 (2004), pp. 267–292.CrossRefGoogle Scholar
[26]Klunder, B., Representable pseudo-interior algebras, Algebra Universalis, vol. 40 (1998), pp. 177–188.CrossRefGoogle Scholar
[27]Kowalski, T., Semisimplicity, EDPC and discriminator varieties of residuated lattices, Studia Logica, vol. 77 (2005), pp. 255–265.CrossRefGoogle Scholar
[28]Kowalski, T. and Paoli, F., On some properties of quasi-MV algebras and quasi-MV algebras. Part III, Reports on Mathematical Logic, vol. 45 (2010), pp. 161–199.Google Scholar
[29]Kowalski, T. and Paoli, F., Joins and subdirect products of varieties, Algebra Universalis, vol. 65 (2011), pp. 371–391.CrossRefGoogle Scholar
[30]Ledda, A., Konig, M., Paoli, F., and Giuntini, R., MV algebras and quantum computation, Studia Logica, vol. 82 (2006), pp. 245–270.CrossRefGoogle Scholar
[31]Mal'cev, A. I., On the general theory of algebraic systems, Matematicheskii Sbornik (N.S.), vol. 35(77) (1954), no. 1, pp. 3–20.Google Scholar
[32]Mc Kenzie, R., An algebraic version of categorical equivalence for varieties and more general algebraic categories, Logic and algebra: Proceedings of the Magari conference (Ursini, A. and Aglianó, P., editors), Dekker, New York, 1996, pp. 211–243.Google Scholar
[33]Mc Kenzie, R., Mc Nulty, G., and Taylor, W., Algebras, lattices, varieties, vol. 1, Wadsworth & Brooks/Cole, Monterey, California, 1987.Google Scholar
[34]Mel'nik, L. I., Nilpotent shifts of varieties, Mathematical Notes, vol. 14 (1973), pp. 692–696.CrossRefGoogle Scholar
[35]Paoli, F., Ledda, A., Giuntini, R., and Freytes, H., On some properties of quasi-MV algebras and quasi-MV algebras. Part I, Reports on Mathematical Logic, vol. 44 (2008), pp. 53–85.Google Scholar
[36]Sambin, G. and Vaccaro, V., Topology and duality in modal logic, Annals of Pure and Applied Logic, vol. 37 (1988), pp. 249–296.CrossRefGoogle Scholar
[37]Spinks, M. and Veroff, R., Constructive logic with strong negation is a substructural logic I, Studia Logica, vol. 88 (2008), pp. 325–348.CrossRefGoogle Scholar
[38]Spinks, M. and Veroff, R., Constructive logic with strong negation is a substructural logic II, Studia Logica, vol. 89 (2008), pp. 401–425.CrossRefGoogle Scholar
[39]Ursini, A., On subtractive varieties I, Algebra Universalis, vol. 31 (1994), pp. 204–222.CrossRefGoogle Scholar
[40]Vakarelov, D., Notes on N-lattices and constructive logic with strong negation, Studia Logica, vol. 36 (1977), pp. 109–125.CrossRefGoogle Scholar
[41]van Alten, C. J., An algebraic study of residuated ordered monoids and logics without exchange and contraction, Ph.D. thesis, University of Natal, 1998.Google Scholar
[42]Werner, H., Discriminator algebras, Akademie Verlag, Berlin, 1978.Google Scholar