Published online by Cambridge University Press: 12 March 2014
In this note I show, by means of an infinite matrix M, that the number of irreducible modalities in Lewis's system S2 is infinite. The result is of some interest in view of the fact that Parry has recently shown that there are but a finite number of modalities in the system S2 (which is the next stronger system than S2 discussed by Lewis).
I begin by introducing a function θ which is defined over the class of sets of signed integers, and which assumes sets of signed integers as values. If A is any set of signed integers, then θ(A) is the set of all signed integers whose immediate predecessors are in A; i.e., 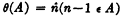 , so that n ϵ θ(A) is true if and only if n − 1 ϵ A is true.
, so that n ϵ θ(A) is true if and only if n − 1 ϵ A is true.
Thus, for example, θ({−10, −1, 0, 3, 14}) = {−9, 0, 1, 4, 15}. In particular we notice that θ(V) = V and θ(Λ) = Λ, where V is the set of all signed integers, and Λ is the empty set of signed integers.
It is clear that, if A and B are sets of signed integers, then θ(A+B) = θ(A)+θ(B).
It is also easily proved that, for any set A of signed integers we have 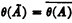 . For, if n is any signed integer, then
. For, if n is any signed integer, then
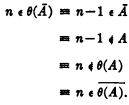
1 Modalities in the Survey system of strict implication, this Journal, vol. 4 (1939), pp. 137–154Google Scholar.
2 See Lewis and Langford's, Symbolic logic, pp. 492–502Google Scholar.