Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T04:10:54.796Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime numbers and factorization in IE1 and weaker systems

Published online by Cambridge University Press:  12 March 2014

Stuart T. Smith
Stuart T. Smith*
Affiliation:
School of Mathematical Sciences, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv, Israel, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that IE1 proves that every element greater than 1 has a unique factorization into prime powers, although we have no way of recovering the exponents from the prime powers which appear. The situation is radically different in Bézout models of open induction. To facilitate the construction of counterexamples, we describe a method of changing irreducibles into powers of irreducibles, and we define the notion of a frugal homomorphism into 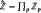, the product of the p-adic integers for each prime p.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 3 , September 1992 , pp. 1057 - 1085
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Bennett, J. H., On spectra, Ph.D. dissertation, Princeton University, Princeton, New Jersey, 1962.Google Scholar
[vdD]van den Dries, L., Some model theory and number theory for models of weak systems of arithmetic, Model theory of algebra and arithmetic (Pacholski, L.et al., editors), Lecture Notes in Mathematics, vol. 834, Springer-Verlag, Berlin, 1980, pp. 346–362.CrossRefGoogle Scholar
[DM]van den Dries, L. and Macintyre, A., The logic of Rumely's local-global principle, Journal für die Reine und Angewandte Mathematik, vol. 407 (1990), pp. 33–56.Google Scholar
[J]Jacobson, N., Basic algebra I, Freeman, San Francisco, California, 1974.Google Scholar
[K]Kaye, R., Diophantine and parameter-free induction, Ph.D. dissertation, University of Manchester, Manchester, 1987.Google Scholar
[L]Lang, S., Algebra, Addison Wesley, Reading, Massachusetts, 1965.Google Scholar
[MM]Macintyre, A. and Marker, D., Primes and their residue rings in models of open induction, Annals of Pure and Applied Logic, vol. 43 (1989), pp. 57–77.CrossRefGoogle Scholar
[PW]Paris, J. and Wilkie, A., Δ0 sets and induction, Open days in model theory and set theory (Proceedings of the Jadwisin, Poland, Logic Conference, 1981); Guzicki, W.et al., editors), Leeds University, Leeds, 1983, pp. 237–248.Google Scholar
[SS]Shamash, J. and Smith, S. T., Embedding GCD domains in Bézout domains, Journal of the London Mathematical Society (to appear).Google Scholar
[Sm1]Smith, S. T., Fermat's last theorem and Bézou's theorem in GCD domains, Journal of Pure and Applied Algebra 79 (1992), 63–85.CrossRefGoogle Scholar
[Sm2]Smith, S. T., Building discretely ordered Bézout domains and GCD domains, Journal of Algebra (to appear).Google Scholar
[Wkl]Wilkie, A. J., Modèles non standard de l'arithmétique, et complexité algorithmique, Modèles non standarden arithmétique et théorie des ensembles, Publications Mathématiques de l'Université Paris-VII, Paris, 1983, pp. 5–45.Google Scholar
[Wk2]Wilkie, A. J., Some results and problems on weak systems of arithmetic, Logic Colloquium '77 (Macintyre, A. J.et al., editors), North-Holland, Amsterdam, 1978, pp. 285–296.CrossRefGoogle Scholar
[Wm]Wilmers, G., Bounded existential induction, this Journal, vol. 50 (1985), pp. 72–90.Google Scholar