Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T18:01:48.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime and atomic models

Published online by Cambridge University Press:  12 March 2014

Julia F. Knight
Julia F. Knight*
Affiliation:
Pennsylvania State University, University Park, PA 16802 University of Notre Dame, Notre Dame, Indiana 46556
Get access Rights & Permissions [Opens in a new window]

Extract

This paper gives some simple existence results on prime and atomic models over sets. It also contains an example in which there is no prime model over a certain set even though there is an atomic model over the set. The existence results are “local” in that they deal with just one set rather than all sets contained in models of some theory. For contrast, see the “global” results in [6] or [7, p. 200].

Throughout the paper, L is a countable language, and T is a complete L-theory with infinite models. There is a “large” model 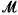of T that contains the set X and any other sets and models to be used in a particular construction of a prime or atomic model over X.

A model 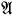is said to be prime over X if 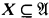and every elementary monomorphism on X can be extended to an elementary embedding on all of 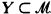. This notion is used in a variety of ways in model theory. It aids in distinguishing between models that are not isomorphic, as in Vaught [10]. It also aids in showing that certain models are isomorphic, as in Baldwin and Lachlan [1].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 3 , September 1978 , pp. 385 - 393
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baldwin, J. T. and Lachlan, A. H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
[2]Baldwin, J. T. and Blass, A., An axiomatic approach to rank in model theory, Annals of Mathematical Logic, vol. 7 (1974), pp. 295–324.CrossRefGoogle Scholar
[3]Harnik, V. and Ressayre, J. P., Prime extensions and categoricity in power, Israel Journal of Mathematics, vol. 10 (1971), pp. 172–185.CrossRefGoogle Scholar
[4]Makkai, M., An admissible generalization of a theorem on countable Σ11-sets with applications, preprint.CrossRefGoogle Scholar
[5]Marcus, L., A minimal model with an infinite set of indiscernibles, Israel Journal of Mathematics, vol. 11 (1972), pp. 180–183.CrossRefGoogle Scholar
[6]Morley, M., Categoricity in power, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–518.CrossRefGoogle Scholar
[7]Sacks, G. E., Saturated model theory, Benjamin, New York, 1972.Google Scholar
[8]Shelah, S., Uniqueness and characterization of prime models over sets for totally transcendental first order theories, this Journal, vol. 37 (1972), pp. 107–113.Google Scholar
[9]Shelah, S., Categoricity in ℵ1, of sentences in Lω1ω(Q), Israel Journal of Mathematics, vol. 20 (1975), pp. 127–148.CrossRefGoogle Scholar
[10]Vaught, R. L., Denumerable models of complete theories, Infinitistic methods, Proceedings of the Symposium on Foundations of Mathematics, Warsaw, 1959, Pergamon Press, Krakow, 1961, PP. 303–321.Google Scholar