Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T11:00:42.675Z Has data issue: false hasContentIssue false
  • English
  • Français

PREDICATIVITY THROUGH TRANSFINITE REFLECTION

Published online by Cambridge University Press:  08 September 2017

ANDRÉS CORDÓN-FRANCO ,
DAVID FERNÁNDEZ-DUQUE ,
JOOST J. JOOSTEN  and
FRANCISCO FÉLIX LARA-MARTÍN
ANDRÉS CORDÓN-FRANCO
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE AND ARTIFICIAL INTELLIGENCE UNIVERSIDAD DE SEVILLA SEVILLE, SPAINE-mail:[email protected]
DAVID FERNÁNDEZ-DUQUE
Affiliation:
CENTRE INTERNATIONAL DE MATHÉMATIQUES ET D’INFORMATIQUE UNIVERSITY OF TOULOUSE TOULOUSE, FRANCE and DEPARTMENT OF MATHEMATICS INSTITUTO TECNOLÓGICO AUTÓNOMO DE MÉXICO, MEXICO MEXICO CITY, MEXICOE-mail:[email protected]
JOOST J. JOOSTEN
Affiliation:
DEPARTMENT OF PHILOSOPHY UNIVERSITY OF BARCELONA BARCELONA, SPAINE-mail:[email protected]
FRANCISCO FÉLIX LARA-MARTÍN
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE AND ARTIFICIAL INTELLIGENCE, UNIVERSIDAD DE SEVILLA SEVILLE, SPAINE-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let T be a second-order arithmetical theory, Λ a well-order, λ < Λ and X ⊆ ℕ. We use 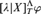$[\lambda |X]_T^{\rm{\Lambda }}\varphi$ as a formalization of “φ is provable from T and an oracle for the set X, using ω-rules of nesting depth at most λ”.

For a set of formulas Γ, define predicative oracle reflection for T over Γ (Pred–O–RFNΓ(T)) to be the schema that asserts that, if X ⊆ ℕ, Λ is a well-order and φ ∈ Γ, then

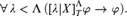$$\forall \,\lambda < {\rm{\Lambda }}\,([\lambda |X]_T^{\rm{\Lambda }}\varphi \to \varphi ).$$

In particular, define predicative oracle consistency (Pred–O–Cons(T)) as Pred–O–RFN{0=1}(T).

Our main result is as follows. Let ATR0 be the second-order theory of Arithmetical Transfinite Recursion, 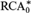${\rm{RCA}}_0^{\rm{*}}$ be Weakened Recursive Comprehension and ACA be Arithmetical Comprehension with Full Induction. Then,

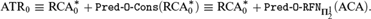$${\rm{ATR}}_0 \equiv {\rm{RCA}}_0^{\rm{*}} + {\rm{Pred - O - Cons\ }}\left( {{\rm{RCA}}_0^{\rm{*}} } \right) \equiv {\rm{RCA}}_0^{\rm{*}} + \,{\rm{Pred - O - Cons\ }}\left( {{\rm{RCA}}_0^{\rm{*}} } \right) \equiv {\rm{RCA}}_0^{\rm{*}} + \,{\rm{Pred - O - RFN}}\,_{{\bf{\Pi }}_2^1 } \left( {{\rm{ACA}}} \right).$$

We may even replace 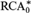${\rm{RCA}}_0^{\rm{*}}$ by the weaker ECA0, the second-order analogue of Elementary Arithmetic.

Thus we characterize ATR0, a theory often considered to embody Predicative Reductionism, in terms of strong reflection and consistency principles.

Keywords

03F4597E3003F03second-order arithmeticreflection principlesprovability logic
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 3 , September 2017 , pp. 787 - 808
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beeson, M. and Ščedrov, A., Church’s thesis, continuity, and set theory, this Journal, vol. 49 (1984), no. 2, pp. 630–643.Google Scholar
Beklemishev, L. D., Induction rules, reflection principles, and provably recursive functions. Annals of Pure and Applied Logic, vol. 85 (1997), pp. 193–242.CrossRefGoogle Scholar
Beklemishev, L. D., Provability algebras and proof-theoretic ordinals, I. Annals of Pure and Applied Logic, vol. 128 (2004), pp. 103–124.CrossRefGoogle Scholar
Beklemishev, L. D., Veblen hierarchy in the context of provability algebras, Logic, Methodology and Philosophy of Science, Proceedings of the Twelfth International Congress (Hájek, P., Valdés-Villanueva, L., and Westerståhl, D., editors), Kings College Publications, London, 2005, pp. 65–78.Google Scholar
Beklemishev, L. D., Reflection principles and provability algebras in formal arithmetic. Russian Mathematical Surveys, vol. 60 (2005), pp. 197–268.Google Scholar
Beklemishev, L. D., The Worm principle, Logic Colloquium 2002 (Chatzidakis, Z., Koepke, P., and Pohlers, W., editors), Lecture Notes in Logic 27, ASL Publications, 2006, pp. 75–95.Google Scholar
Beklemishev, L. D., On the reduction property for GLP-algebras. Doklady: Mathematics, vol. 472 (2017), no. 4.Google Scholar
Beklemishev, L. D., Fernández-Duque, D., and Joosten, J. J., On provability logics with linearly ordered modalities. Studia Logica, vol. 102 (2014), pp. 541–566.Google Scholar
Beklemishev, L. D. and Onoprienko, A. A., On some slowly terminating term rewriting systems. Sbornik: Mathematics, vol. 206 (2015), no. 9, pp. 1173–1190.Google Scholar
Boolos, G. S., The Logic of Provability, Cambridge University Press, Cambridge, 1993.Google Scholar
Cordón-Franco, A., Fernández-Margarit, A., and Lara-Martín, F. F., Fragments of Arithmetic and true sentences. Mathematical Logic Quarterly, vol. 51 (2005), pp. 313–328.CrossRefGoogle Scholar
Feferman, S., Systems of predicative analysis, this Journal, vol. 29 (1964), pp. 1–30.Google Scholar
Feferman, S., Systems of predicative analysis II, this JOURNAL, vol. 33 (1968), pp. 193–220.Google Scholar
Fernández-Duque, D., The polytopologies of transfinite provability logic. Archive for Mathematical Logic, vol. 53 (2014), no. 3–4, pp. 385–431.CrossRefGoogle Scholar
Fernández-Duque, D. and Joosten, J. J., Models of transfinite provability logics, this Journal, vol. 78 (2013), no. 2, pp. 543–561.Google Scholar
Fernández-Duque, D. and Joosten, J. J., The omega-rule interpretation of transfinite provability logic, (2013), arXiv, vol. 1205.2036 [math.LO].Google Scholar
Fernández-Duque, D. and Joosten, J. J., Well-orders in the transfinite Japaridze algebra. Logic Journal of the Interest Group in Pure and Applied Logic, vol. 22 (2014), no. 6, pp. 933–963.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First Order Arithmetic, Springer-Verlag, Berlin, Heidelberg, New York, 1993.Google Scholar
Hirst, J. L., A survey of the reverse mathematics of ordinal arithmetic, Reverse mMathematics 2001, Lecture Notes in Logic, vol. 21, Peters, A. K., Natick, MA, 2005, pp. 222–234.Google Scholar
Ignatiev, K. N., On strong provability predicates and the associated modal logics, this Journal, vol. 58 (1993), pp. 249–290.Google Scholar
Japaridze, G., The polymodal provability logic, Intensional Logics and Logical Structure of Theories: Material from the Fourth Soviet-Finnish Symposium on Logic, Metsniereba, Telaviv, 1988, pp. 16–48, In Russian.Google Scholar
Joosten, J. J., . ${\rm{\Pi }}_1^0$ -ordinal analysis beyond first-order arithmetic. Mathematical Communications, vol. 18 (2013), pp. 109–121.Google Scholar
Kreisel, G. and Lévy, A., Reflection principles and their use for establishing the complexity of axiomatic systems. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 97–142.Google Scholar
Leivant, D., The optimality of induction as an axiomatization of arithmetic, this Journal, vol. 48 (1983), pp. 182–184.Google Scholar
Schmerl, U. R., A fine structure generated by reflection formulas over primitive recursive arithmetic, Logic Colloquium ’78 (Mons, 1978) (Boffa, M., Dalen, D., and Mcaloon, K., editors), Studies in Logic and the Foundations of Mathematics, vol. 97, North-Holland, Amsterdam, 1979, pp. 335–350.Google Scholar
Simpson, S. G., Friedman’s research on subsystems of second-order arithmetic, Harvey Friedman’s Research in the Foundations of Mathematics (Harrington, L., Morley, M., Ščedrov, A, and Simpson, S. G., editors), North-Holland, Amsterdam, 1985, pp. 137–159.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Cambridge University Press, New York, 2009.Google Scholar
Simpson, S. G. and Smith, R. L., Factorization of polynomials and ${\rm{\Sigma }}_1^0$ induction. Annals of Pure and Applied Logic, vol. 31 (1986), pp. 289–306.Google Scholar
Tait, W., Finitism. Journal of Philosophy, vol. 78 (1981), pp. 524–546.Google Scholar