Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T17:02:00.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Possible behaviours of the reflection ordering of stationary sets

Published online by Cambridge University Press:  12 March 2014

Jiří Witzany
Jiří Witzany*
Affiliation:
Department of Mathematics, University of California, Los Angeles, California 90024-1555, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If S, T are stationary subsets of a regular uncountable cardinal κ, we say that S reflects fully in T, S < T, if for almost all α ∈ T (except a nonstationary set) S ∩ α stationary in α. This relation is known to be a well-founded partial ordering. We say that a given poset P is realized by the reflection ordering if there is a maximal antichain 〈Xp: p ∈ P〉 of stationary subsets of Reg(κ) so that

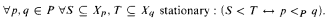
We prove that if 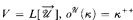, and P is an arbitrary well-founded poset of cardinality ≤ κ+ then there is a generic extension where P is realized by the reflection ordering on κ.

Keywords

Primary 03E3503E55.Stationary setsreflectionmeasurable cardinalsrepeat points
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 2 , June 1995 , pp. 534 - 547
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[J84]Jech, T., Stationary subsets of inaccessible cardinals, Axiomatic set theory, (Baumgartner, J. E.et al., editors), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, Rhode Island, 1984, pp. 115–141.Google Scholar
[J86]Jech, T., Multiple forcing, Cambridge University Press, Cambridge, 1986.Google Scholar
[J89]Jech, T., Positive Σ operations on cardinals and normal filters on greatly Mahlo cardinals, this Journal, vol. 54 (1989), pp. 226–233.Google Scholar
[JS90]Jech, T. and Shelah, S., Full reflection of stationary sets below ℵω, this Journal, vol. 55 (1990), pp. 822–829.Google Scholar
[JS93]Jech, T. and Shelah, S., Full reflection of stationary sets at regular cardinals, American Journal of Mathematics, vol. 115 (1993), pp. 435–453.CrossRefGoogle Scholar
[JW94]Jech, T. and Witzany, J., Full reflection at a measurable cardinal, this Journal, vol. 59 (1994), pp. 615–630.Google Scholar
[Ka9X]Kanamori, A., The higher infinite. I, II, in preparation.Google Scholar
[La78]Laver, R., Making supercompactness of κ undestructible under κ-directed closed forcing, Israel Journal of Mathematics, vol. 29 (1978), pp. 385–388.CrossRefGoogle Scholar
[M82]Magidor, M., Reflecting stationary sets, this Journal, vol. 47 (1982), pp. 755–771.Google Scholar
[Mi83]Mitchell, W. J., Sets constructive from sequences of measures; revisited, this Journal, vol. 48 (1983), pp. 600–609.Google Scholar
[WoC9X]Woodin, H. and Cummings, J., Generalised Prikry forcings, in preparation.Google Scholar