Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-20T01:02:08.238Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise compact and stable sets of measurable functions

Published online by Cambridge University Press:  12 March 2014

S. Shelah  and
D. H. Fremlin
S. Shelah
Affiliation:
Hebrew University, Jerusalem, E-mail: [email protected]
D. H. Fremlin
Affiliation:
University of Essex, Colchester, England, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In a series of papers culminating in [9], M. Talagrand, the second author, and others investigated at length the properties and structure of pointwise compact sets of measurable functions. A number of problems, interesting in themselves and important for the theory of Pettis integration, were solved subject to various special axioms. It was left unclear just how far the special axioms were necessary. In particular, several results depended on the fact that it is consistent to suppose that every countable relatively pointwise compact set of Lebesgue measurable functions is ‘stable’ in Talagrand's sense, the point being that stable sets are known to have a variety of properties not shared by all pointwise compact sets. In the present paper we present a model of set theory in which there is a countable relatively pointwise compact set of Lebesgue measurable functions which is not stable and discuss the significance of this model in relation to the original questions. A feature of our model which may be of independent interest is the following: in it, there is a closed negligible set Q ⊆ [0, 1]2 such that whenever D ⊆ [0,1] has outer measure 1, then

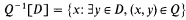
has inner measure 1 (see 2G below).

We embark immediately on the central ideas of this paper, setting out a construction of a partially ordered set which forces a fairly technical proposition in measure theory (IS below); the relevance of this proposition to pointwise compact sets will be discussed in §2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 58 , Issue 2 , June 1993 , pp. 435 - 455
Copyright
Copyright © Association for Symbolic Logic 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bartoszyński, T., Judah, H., and Shelah, S., The Cichoń diagram, preprint, 1989. (MSRI 00626-90)Google Scholar
[2]Baumgartner, J. E., Applications of the proper forcing axiom, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984, pp. 913–959.CrossRefGoogle Scholar
[3]Friedman, H., Rectangle inclusion problems, Note of 9 10 1989.Google Scholar
[4]Kunen, K., Set Theory, North-Holland, Amsterdam, 1980.Google Scholar
[5]Kunen, K. and Vaughan, J. E. (editors), Handbook of set-theoretic topology, North-Holland, Amsterdam, 1984.Google Scholar
[6]Shelah, S., Proper forcing, Lecture Notes in Mathematics, vol. 940, Springer-Verlag, Berlin, 1982.CrossRefGoogle Scholar
[7]Shelah, S., Vive la différence, I, Proceedings of the Conference in Set theory (Judah, H., Just, W., and Woodin, H., editors), Springer-Verlag, 1992, pp. 357–405.Google Scholar
[8]Spencer, J., Ten lectures on the probabilistic method, CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 52, Society for Industrial and Applied Mathematics, 1987.Google Scholar
[9]Talagrand, M., Pettis integral and measure theory, Memoirs of the American Mathematical Society, vol. 307, American Mathematical Society, Providence, Rhode Island, 1984.Google Scholar
[10]Talagrand, M., The Glivenko-Cantelli problem, The Annals of Probability, 15 (1987), pp. 837–870.CrossRefGoogle Scholar