Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T05:15:23.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial impredicativity in reverse mathematics

Published online by Cambridge University Press:  12 March 2014

Henry Towsner
Henry Towsner*
Affiliation:
Department of Mathematics, University of Pennsylvania, 209 South 33rd Street, Philadelphia, PA 19104-6395, USA, E-mail:[email protected], URL: www.math.upenn.edu/~htowsner
Get access Rights & Permissions [Opens in a new window]

Abstract

In reverse mathematics, it is possible to have a curious situation where we know that an implication does not reverse, but appear to have no information on how to weaken the assumption while preserving the conclusion (other than reducing all the way to the tautology of assuming the conclusion). A main cause of this phenomenon is the proof of a 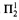sentence from the theory . Using methods based on the functional interpretation, we introduce a family of weakenings of and use them to give new upper bounds for the Nash-Williams Theorem of wqo theory and Menger's Theorem for countable graphs.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 2 , June 2013 , pp. 459 - 488
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Avigad, Jeremy, An effective proof that open sets are Ramsey, Archive for Mathematical Logic, vol. 37 (1998), no. 4, pp. 235–240.CrossRefGoogle Scholar
[2]Avigad, Jeremy and Feferman, Solomon, Gödel's functional (“Dialectica”) interpretation, Handbook of proof theory. Studies in Logic and the Foundations of Mathematics, vol. 137, North-Holland, Amsterdam, 1998, pp. 337–405.CrossRefGoogle Scholar
[3]Avigad, Jeremy and Towsner, Henry. Functional interpretation and inductive definitions, this Journal, vol. 74 (2009), no. 4, pp. 1100–1120.Google Scholar
[4]Cholak, Peter A., Jockusch, Carl G.. and Slaman, Theodore A., On the strength of Ramsey's theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
[5]Clote, Peter, A recursion theoretic analysis of the clopen Ramsey theory, this Journal, vol. 49 (1984), no. 2. pp. 376–400.Google Scholar
[6]Friedman, Harvey M.. McAloon, Kenneth. and Simpson, Stephen G., A finite combinatorial principle which is equivalent to the 1-consistency of predicative analysis, Patras Logic Symposion, Studies in Logic and the Foundations of Mathematics, vol. 109, North-Holland, Amsterdam, 1982, pp. 197–230.CrossRefGoogle Scholar
[7]Kohlenbach, U., Applied proof theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2008.Google Scholar
[8]Marcone, Alberto, On the logical strength of Nash-Williams' theorem on transfinite sequences. Logic: from foundations to applications, Oxford University Press, 1996, pp. 327–351.CrossRefGoogle Scholar
[9]Nash-Williams, C. St. J. A., On well-quasi-ordering finite trees, Proceedings of the Cambridge Philosophical Society, vol. 59 (1963), pp. 833–835.CrossRefGoogle Scholar
[10]Pohlers, Wolfram, Subsystems of set theory and second order number theory. Handbook of proof theory, Studies in Logic and the Foundations of Mathematics, vol. 137, North-Holland, Amsterdam, 1998, pp. 209–335.CrossRefGoogle Scholar
[11]Rathjen, Michael and Weiermann, Andreas, Proof-theoretic investigations on Kruskal's theorem, Annuls of Pure and Applied Logic, vol. 60 (1993), no. 1, pp. 49–88.CrossRefGoogle Scholar
[12]Schütte, Kurt and Simpson, Stephen G., Ein in der reinen Zahlentheorie unbeweisbarer Satz über endliche Folgen von natürlichen Zahlen, Archiv für Mathematische Logik und Grundlagenforschung, vol. 25 (1985), no. 1–2, pp. 75–89.CrossRefGoogle Scholar
[13]Shafer, Paul, Menger's theorem in , Archive for Mathematical Logic, vol. 51 (2012), no. 3–4, pp. 407–423.CrossRefGoogle Scholar
[14]Simpson, Stephen G., Ordinal numbers and the Hilbert basis theorem, this Journal, vol. 53 (1988), no. 3, pp. 961–974.Google Scholar
[15]Simpson, Stephen G., Subsystems of second order arithmetic, second ed., Perspectives in Logic. Association for Symbolic Logic and Cambridge University Press, 2009.CrossRefGoogle Scholar