Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T05:08:30.698Z Has data issue: false hasContentIssue false
  • English
  • Français

Pair-splitting, pair-reaping and cardinal invariants of Fσ-ideals

Published online by Cambridge University Press:  12 March 2014

Michael Hrušák ,
David Meza-Alcántara  and
Hiroaki Minami
Michael Hrušák
Affiliation:
Instituto de Matemáticas, Unam, Apartado Postal 61-3, Xangari 58089, Morelia, michoacán, México. E-mail: [email protected]
David Meza-Alcántara
Affiliation:
Instituto de Matemáticas, Unam, Apartado Postal 61-3, Xangari 58089, Morelia, michoacán, México. E-mail: [email protected]
Hiroaki Minami
Affiliation:
Kurt Gödel Research Center for Mathematical Logic Währinger Straße 25 A-1090 Wien, Austria. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

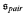We investigate the pair-splitting number which is a variation of splitting number, pair-reaping number 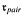which is a variation of reaping number and cardinal invariants of ideals on ω. We also study cardinal invariants of Fσ ideals and their upper bounds and lower bounds. As an application, we answer a question of S. Solecki by showing that the ideal of finitely chromatic graphs is not locally Katětov-minimal among ideals not satisfying Fatou's lemma.

Keywords

Pair-splitting numberpair-reaping numbercardinal invariants of the continuumFσ-idealsLaver forcing
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 2 , June 2010 , pp. 661 - 677
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balcar, B., Hernández-Hernández, F., and Hrušák, M., Combinatorics of dense subsets of the rationals, Fundamenta Mathematicae, vol. 183 (2004), no. 1, pp. 59–80.CrossRefGoogle Scholar
[2]Bartoszyński, Tomek and Judah, Haim, Set theory. On the structure of the real line, A K Peters, Wellesley, MA, 1995.Google Scholar
[3]Blass, Andreas, Combinatorial cardinal characteristics of the continuum, Handbook of set theory (Foreman, Matthew and Kanamori, Akihiro, editors), Springer-Verlag, Berlin, to appear.Google Scholar
[4]Goldstern, Martin, Tools for your forcing construction. Set theory of the reals (Judah, Haim, editor), Israel Mathematical Conference Proceedings, vol. 6, American Mathematical Society, 1991, pp. 305–360.Google Scholar
[5]Hernández-Hernández, Fernando and Hrušák, Michael, Cardinal invariants of analytic P-ideals, Canadian Journal of Mathematics, vol. 59 (2007), no. 3, pp. 575–595.CrossRefGoogle Scholar
[6]Hrušák, Michael and Ferreira, Salvador García, Ordering MAD families a la Katétov, this Journal, vol. 68 (2003), no. 4, pp. 1337–1353.Google Scholar
[7]Kada, Masaru, More on Cichoń's diagram and infinite games, this Journal, vol. 65 (2000), no. 4. pp. 1713–1724.Google Scholar
[8]Kurilić, Miloš S., Cohen-stable families of subsets of integers, this Journal, vol. 66 (2001), no. 1, pp. 247–270.Google Scholar
[9]Laflamme, Claude, Zapping small filters, Proceedings of the American Mathematical Society, vol. 114 (1992), no. 2, pp. 535–544.CrossRefGoogle Scholar
[10]Mazur, Krzysztof, Fσ-ideals and ω1ω1*-gaps in the boolean algebras , Fundamenta Mathematicae, vol. 138 (1991), no. 2, pp. 103–111.CrossRefGoogle Scholar
[11]Mildenberger, Heike, Non-constructive Galois–Tukey connections, this Journal, vol. 62 (1997), no. 4, pp. 1179–1186.Google Scholar
[12]Mildenberger, Heike, No Borel connections for the unsplitting relations, Mathematical Logic Quarterly, vol. 48 (2002), no. 4, pp. 517–521.3.0.CO;2-#>CrossRefGoogle Scholar
[13]Minami, Hiroaki, Around splitting and reaping number for partitions of ω, submitted 08 2007.Google Scholar
[14]Minami, Hiroaki, On pair-splitting and pair-reaping pairs of ω, preprint.Google Scholar
[15]Solecki, Sławomir, Filters and sequences, Fundamenta Mathematicae, vol. 163 (2000), no. 3, pp. 215–228.CrossRefGoogle Scholar
[16]Vojtáš, Peter, Generalized Galois–Tukey-connections between explicit relations on classical objects of real analysis, Set theory of the reals, Israel Mathematical Conference Proceedings, vol. 6, 1993, pp. 619–643.Google Scholar