Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vassiliev, Evgueni
2003.
Generic pairs of SU-rank 1 structures.
Annals of Pure and Applied Logic,
Vol. 120,
Issue. 1-3,
p.
103.


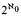 completions, that is, the maximum that could exist.
completions, that is, the maximum that could exist.