Published online by Cambridge University Press: 12 March 2014
The notion of the next admissible set has proved to be a very useful notion in definability theory and generalized recursion theory, a unifying notion that has produced further interesting results in its own right. The basic treatment of the next admissible set 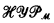 above a structure ℳ of urelements is to be found in Barwise's [75] book Admissible sets and structures. Also to be found there are many of the interesting characterizations of the next admissible set. For further justification of the interest of the next admissible set the reader is referred to Moschovakis [74], Nadel and Stavi [76] and Schlipf [78a, b, c].
above a structure ℳ of urelements is to be found in Barwise's [75] book Admissible sets and structures. Also to be found there are many of the interesting characterizations of the next admissible set. For further justification of the interest of the next admissible set the reader is referred to Moschovakis [74], Nadel and Stavi [76] and Schlipf [78a, b, c].
One of the most interesting single properties of 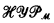 is its ordinal
is its ordinal 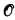 (ℳ). It coincides, for example, with Moschovakis' inductive closure ordinal over structures ℳ with pairing functions—and over some, such as algebraically closed fields of characteristic 0, without pairing functions (by recent work of Arthur Rubin) (although a locally famous counterexample of Kunen, a theorem of Barwise [77], and some recent results of Rubin and the author, show that the inductive closure ordinal may also be strictly smaller in suitably pathological structures). Further justification for looking at
(ℳ). It coincides, for example, with Moschovakis' inductive closure ordinal over structures ℳ with pairing functions—and over some, such as algebraically closed fields of characteristic 0, without pairing functions (by recent work of Arthur Rubin) (although a locally famous counterexample of Kunen, a theorem of Barwise [77], and some recent results of Rubin and the author, show that the inductive closure ordinal may also be strictly smaller in suitably pathological structures). Further justification for looking at 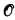 (ℳ) alone may be found in the above-listed references. Loosely, we can consider the size of
(ℳ) alone may be found in the above-listed references. Loosely, we can consider the size of 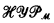 to be a useful measure of the complexity of ℳ. One of the simplest measures of the size of
to be a useful measure of the complexity of ℳ. One of the simplest measures of the size of 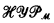 —and yet a very useful measure—is its ordinal,
—and yet a very useful measure—is its ordinal, 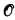 (ℳ). Keisler has suggested thinking of
(ℳ). Keisler has suggested thinking of 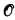 (ℳ) as the information content of a model—the supremum of lengths of wellfounded relations characterizable in the model.
(ℳ) as the information content of a model—the supremum of lengths of wellfounded relations characterizable in the model.
This paper is an expansion of a talk given by the author to the Association for Symbolic Logic at Reno, Nevada, on April 24, 1976. Several of the basic results were contained in the author's doctoral dissertation at the University of Wisconsin (Schhpf [75]). The results of Kunen mentioned here are as yet unpublished. The author is particularly indebted to Professors K. Kunen and J. Barwise for the help they gave him while he did the early research on this topic for his doctoral thesis.