Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leivant, Daniel
1982.
Unprovability of theorems of complexity theory in weak number theories.
Theoretical Computer Science,
Vol. 18,
Issue. 3,
p.
259.
Sieg, Wilfried
1985.
Fragments of arithmetic.
Annals of Pure and Applied Logic,
Vol. 28,
Issue. 1,
p.
33.
Ono, Hiroakira
1987.
Reflection Principles in Fragments of Peano Arithmetic.
Mathematical Logic Quarterly,
Vol. 33,
Issue. 4,
p.
317.
Beklemishev, Lev D.
1997.
Induction rules, reflection principles, and provably recursive functions.
Annals of Pure and Applied Logic,
Vol. 85,
Issue. 3,
p.
193.
Beklemishev, Lev D.
1999.
Parameter free induction and provably total computable functions.
Theoretical Computer Science,
Vol. 224,
Issue. 1-2,
p.
13.
Artemov, Sergei N.
and
Beklemishev, Lev D.
2005.
Handbook of Philosophical Logic, 2nd Edition.
Vol. 13,
Issue. ,
p.
189.
Cordón-Franco, Andrés
Fernández-Margarit, Alejandro
and
Lara-Martín, F. Félix
2005.
Fragments of Arithmetic and true sentences.
Mathematical Logic Quarterly,
Vol. 51,
Issue. 3,
p.
313.
Joosten, Joost J.
2005.
The Closed Fragment of the Interpretability Logic of PRA with a Constant for $\mathrm{I}\Sigma_1$.
Notre Dame Journal of Formal Logic,
Vol. 46,
Issue. 2,
Беклемишев, Лев Дмитриевич
and
Beklemishev, Lev Dmitrievich
2005.
Схемы рефлексии и алгебры доказуемости в формальной арифметике.
Успехи математических наук,
Vol. 60,
Issue. 2,
p.
3.
Shavrukov, V. Yu.
and
Visser, Albert
2014.
Uniform Density in Lindenbaum Algebras.
Notre Dame Journal of Formal Logic,
Vol. 55,
Issue. 4,
Beklemishev, L. D.
2015.
Turing’s Revolution.
p.
225.
Dean, W.
2015.
Arithmetical Reflection and the Provability of Soundness.
Philosophia Mathematica,
Vol. 23,
Issue. 1,
p.
31.
CORDÓN-FRANCO, ANDRÉS
FERNÁNDEZ-DUQUE, DAVID
JOOSTEN, JOOST J.
and
LARA-MARTÍN, FRANCISCO FÉLIX
2017.
PREDICATIVITY THROUGH TRANSFINITE REFLECTION.
The Journal of Symbolic Logic,
Vol. 82,
Issue. 3,
p.
787.
Beklemishev, Lev D.
2017.
Logic Colloquium '02.
p.
75.
Kolmakov, Evgeny
2020.
Local reflection, definable elements and 1-provability.
Archive for Mathematical Logic,
Vol. 59,
Issue. 7-8,
p.
979.
Fernández-Duque, David
Papafilippou, Konstnatinos
and
Joosten, Joost J.
2022.
Logical Foundations of Computer Science.
Vol. 13137,
Issue. ,
p.
52.
FernÁndez-Duque, David
Joosten, Joost J
Pakhomov, Fedor
Papafilippou, Konstantinos
and
Weiermann, Andreas
2022.
Arithmetical and Hyperarithmetical Worm Battles.
Journal of Logic and Computation,
Vol. 32,
Issue. 8,
p.
1558.
FRITTAION, EMANUELE
2022.
A NOTE ON FRAGMENTS OF UNIFORM REFLECTION IN SECOND ORDER ARITHMETIC.
The Bulletin of Symbolic Logic,
Vol. 28,
Issue. 3,
p.
451.
Beklemishev, Lev D.
and
Pakhomov, Fedor N.
2022.
Reflection algebras and conservation results for theories of iterated truth.
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 5,
p.
103093.
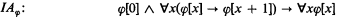
 be the schema IAφ for φ in Πn (i.e.
be the schema IAφ for φ in Πn (i.e.  ); similarly for
); similarly for 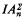 . Each instance of
. Each instance of  is Δn+2, and each instance of
is Δn+2, and each instance of 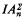 is Σn+1 Thus the universal closure
is Σn+1 Thus the universal closure  of an instance α is Πn+2 in either case. Charles Parsons [72] proved that
of an instance α is Πn+2 in either case. Charles Parsons [72] proved that  and
and 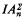 are equivalent over Z0, where Z0 is essentially Primitive Recursive Arithmetic augmented by classical First Order Logic [Parsons 70].
are equivalent over Z0, where Z0 is essentially Primitive Recursive Arithmetic augmented by classical First Order Logic [Parsons 70].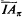 is not derivable in Z0from
is not derivable in Z0from