Published online by Cambridge University Press: 12 March 2014
The purpose of this paper is to give a partial answer to the question: How much is the induction axiom weakened if it is applied only to sentences with no bound variables? It is well known that for the full Peano arithmetic this is a weakening ([1] p. 90). We consider Peano arithmetic without multiplication, and give a full answer to the question. It turns out that only four new theorems can be proved from the weakened induction axiom; i.e., all further consequences of this axiom are derivable from these four.
We consider a system T formulated within the first-order predicate calculus with equality. The system contains the constant 0 and the three function symbols S (successor), P (predecessor), and +. The non-logical axioms are:
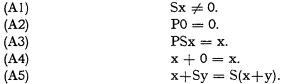
A sentence is open if it contains no bound variables. We obtain the system TI from T by adding the rule of inference:
(I) If A(x) is an open sentence, infer A(x) from A(0) and A(x) ⊃ A(Sx).
The following open sentences are easily proved in TI:
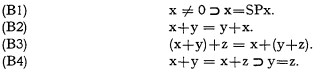
The system formed by adding (B1) - (B4) to T is called T′.
We abbreviate SS … Sx, where S occurs n times, to Snx. Similarly, we abbreviate (… (x+x)+ …) + x, where x occurs n times, to nx. A term of the form n1x1 + … + nkXk + Sp0 is called simple. An equation between simple terms is called a simple equation.
Presented to the Association for Symbolic Logic, December 27, 1956. This research was supported by the National Science Foundation. The author would like to thank G. Kreisel for suggestions and advice.