In [3], Shelah defined the cardinals κn(T) and 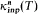, for each theory T and n < ω. κn(T) is the least cardinal κ without a sequence (pi)i<κ of complete n-types such that pi is a forking extension of pj for all i < j < κ. It is essential in computing the stability spectrum of a stable theory. On the other hand 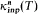is called the number of independent partitions of T. (See Definition 1.2 below.) Unfortunately this invariant has not been investigated deeply. In the author's opinion, this unfortunate situation of 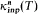is partially due to the fact that its definition is complicated in expression. In this paper, we shall give equivalents of 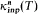which can be easily handled.

In §1 we shall state the definitions of κn(T) and 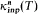. Some basic properties of forking will be stated in this section. We shall also show that if 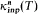= ∞ then T has the independence property.

In §2 we shall give some conditions on κ, n, and T which are equivalent to the statement 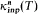. (See Theorem 2.1 below.) We shall show that 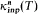does not depend on n. We introduce the cardinal ı(T), which is essential in computing the number of types over a set which is independent over some set, and show that ı(T) is closely related to 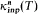. (See Theorems 2.5 and 2.6 below.) The author expects the reader will discover the importance of 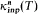via these theorems.

Some of our results are motivated by exercises and questions in [3, Chapter III, §7]. The author wishes to express his heartfelt thanks to the referee for a number of helpful suggestions.