Article contents
On the interpolation theorem for the logic of constant domains
Published online by Cambridge University Press: 12 March 2014
Extract
In Gabbay [1] it is stated as an open problem whether or not Craig's Theorem holds for the logic of constant domains CD, i.e. for the extension of the intuitionistic predicate calculus, IPC, obtained by adding the schema; 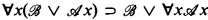 . Then in the later article, [2], Gabbay gives a proof of it. The proof given in [2] is via Robinson's (weak) consistency theorem and depends on relatively complicated (Kripke-) model-theoretical constructions developed in [1] (see p. 392 of [1] for a brief sketch of the method). The aim of this note is to show that the interpolation theorem for CD can also be obtained, by simple proof-theoretic methods, from §80 of Kleene's Introduction to Metamathematics [3].
. Then in the later article, [2], Gabbay gives a proof of it. The proof given in [2] is via Robinson's (weak) consistency theorem and depends on relatively complicated (Kripke-) model-theoretical constructions developed in [1] (see p. 392 of [1] for a brief sketch of the method). The aim of this note is to show that the interpolation theorem for CD can also be obtained, by simple proof-theoretic methods, from §80 of Kleene's Introduction to Metamathematics [3].
GI is the classical formal system whose postulates are given on p. 442 of [3]. Let GD be the system obtained from GI by the following modifications: (1) the sequents of GD are to have at most two formulas in their succedents and (2) the intuitionistic restriction that Θ be empty is required for the succedent rules (→ ¬) and (→ ⊃). It is a simple matter to show that: 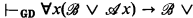
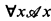 , x not free in
, x not free in 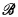 . It then follows that, using Theorem 46 of [3], if
. It then follows that, using Theorem 46 of [3], if 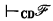 then
then 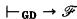 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 5
- Cited by


