No CrossRef data available.
Article contents
On the Hanf number of Souslin logic1
Published online by Cambridge University Press: 12 March 2014
Abstract
We show it is consistent with ZFC that the Hanf number of Ellentuck's Souslin logic should be exactly 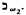 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
Footnotes
1
Research supported by NSF MCS 76-10224.
References
BIBLIOGRAPHY
[1]Barwise, K. J., Absolute logics and L∞,ω, Annals of Mathematical Logic, vol. 4 (1972), pp. 309–349.CrossRefGoogle Scholar
[2]Burgess, J. P., Infinitary languages and descriptive set theory, Doctoral dissertation, University of California, Berkeley, 1974.Google Scholar
[3]Burgess, J. P., Descriptive set theory and infinitary languages, Proceedings of the Belgrade Symposium on Set Theory and Foundations of Mathematics (to appear).Google Scholar
[4]Ellentuck, E., Foundations of Souslin logic, this Journal, vol. 40 (1975), pp. 567–575.Google Scholar
[6]Martin, D. A. and Solovay, R. M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[7]Vaught, R. L., Invariant sets in topology and logic, Fundamenta Mathematicae, vol. 82 (1974), pp. 270–294.CrossRefGoogle Scholar


