Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T10:34:43.691Z Has data issue: false hasContentIssue false
  • English
  • Français

On the expressiveness of frame satisfiability and fragments of second-order logic

Published online by Cambridge University Press:  12 March 2014

Thomas Eiter  and
Georg Gottlob
Thomas Eiter
Affiliation:
Information Systems Department, Tu Vienna, Paniglgasse 16, A-1040, Wien, Austria, E-mail: [email protected]
Georg Gottlob
Affiliation:
Information Systems Department, Tu Vienna, Paniglgasse 16, A-1040, Wien, Austria, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It was conjectured by Halpern and Kapron (Annals of Pure and Applied Logic, vol. 69, 1994) that frame satisfiability of propositional modal formulas is incomparable in expressive power to both 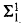(Ackermann) and 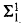(Bernays-Schönfinkel). We prove this conjecture. Our results imply that 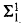(Ackermann) and 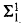(Bernays-Schönfinkel) are incomparable in expressive power, already on finite graphs. Moreover, we show that on ordered finite graphs, i.e., finite graphs with a successor, 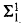(Bernays-Schönfinkel) is strictly more expressive than 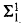(Ackermann).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 1 , March 1998 , pp. 73 - 82
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]van Benthem, J., Modal logic and classical logic, Bibliopolis, Naples, 1983.Google Scholar
[2]Büchi, J., Weak second-order logic and finite automata, Z. Math. Logik Grundlagen Math., vol. 5 (1960), pp. 66–92.CrossRefGoogle Scholar
[3]Chang, C. C. and Keisler, H. J., Model theory, 2nd ed., North-Holland, 1973.Google Scholar
[4]Eiter, T., Gottlob, G., and Gurevich, Y., Normal forms for second-order logic over finite structures, and classification of NP optimization problems, Annals of Pure and Applied Logic, vol. 78 (1996), pp. 111–125.CrossRefGoogle Scholar
[5]Fagin, R., Generalized first-order spectra and polynomial-time recognizable sets, Complexity of computation (Karp, R. M., editor), American Mathematical Society, 1974, pp. 43–74.Google Scholar
[6]Fagin, R., Probabilities on finite models, this Journal, vol. 41 (1976), pp. 50–58.Google Scholar
[7]Glebskii, Y., Kogan, D., Liogon'kii, M., and Talanov, V., Range and degree of realizibility of formulas in the restricted predicate calculus, Kibernetika (1969), pp. 17–28.Google Scholar
[8]Halpern, J. and Kapron, B., Zero-one laws for modal logic, Annals of Pure and Applied Logic, vol. 69 (1994), pp. 57–193.CrossRefGoogle Scholar
[9]Kolaitis, P. and Vardi, M. Y., 0-1 laws and decision problems for fragments of second-order logic, Information and Computation, vol. 87 (1990), pp. 302–338.CrossRefGoogle Scholar
[10]Leivant, D., Descriptive characterizations of computational complexity, Journal of Computer and System Sciences, vol. 39 (1989), pp. 51–83.CrossRefGoogle Scholar