Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T13:57:24.580Z Has data issue: false hasContentIssue false
  • English
  • Français

On the elementary theory of pairs of real closed fields. II

Published online by Cambridge University Press:  12 March 2014

Walter Baur
Walter Baur*
Affiliation:
Seminar for Applied Mathematics, University of Zurich, Zurich, Switzerland
Get access Rights & Permissions [Opens in a new window]

Extract

Let ℒ be the first order language of field theory with an additional one place predicate symbol. In [B2] it was shown that the elementary theory T of the class 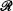of all pairs of real closed fields, i.e., ℒ-structures ‹K, L›, K a real closed field, L a real closed subfield of K, is undecidable.

The aim of this paper is to show that the elementary theory Ts of a nontrivial subclass of 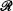containing many naturally occurring pairs of real closed fields is decidable (Theorem 3, §5). This result was announced in [B2]. An explicit axiom system for Ts will be given later. At this point let us just mention that any model of Ts, is elementarily equivalent to a pair of power series fields ‹R0((TA)), R1((TB))› where R0 is the field of real numbers, R1 = R0 or the field of real algebraic numbers, and B ⊆ A are ordered divisible abelian groups. Conversely, all these pairs of power series fields are models of Ts.

Theorem 3 together with the undecidability result in [B2] answers some of the questions asked in Macintyre [M]. The proof of Theorem 3 uses the model theoretic techniques for valued fields introduced by Ax and Kochen [A-K] and Ershov [E] (see also [C-K]). The two main ingredients are

(i) the completeness of the elementary theory of real closed fields with a distinguished dense proper real closed subfield (due to Robinson [R]),

(ii) the decidability of the elementary theory of pairs of ordered divisible abelian groups (proved in §§1-4).

I would like to thank Angus Macintyre for fruitful discussions concerning the subject. The valuation theoretic method of classifying theories of pairs of real closed fields is taken from [M].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 47 , Issue 3 , September 1982 , pp. 669 - 679
Copyright
Copyright © Association for Symbolic Logic 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[A] Ax, J., A metamathematical approach to some problems in number theory, Proceedings of Symposia in Pure Mathematics, vol.20, American Mathematical Society, Providence, RI, 1971, pp. 161–190.Google Scholar
[A-K] Ax, J. and Kochen, S., Diophantine problems over local fields. I, II, III, American Journal of Mathematics, vol. 87 (1965), pp. 605–630, 631–648; Annals of Mathematics, vol. 83 (1966), pp. 437–456.CrossRefGoogle Scholar
[Bl] Baur, W., Undecidability of the theory of abelian groups with a subgroup, Proceedings of the American Mathematical Society, vol. 55 (1976), pp. 125–128.CrossRefGoogle Scholar
[B2] Baur, W., Die Theorie der Paare reell abgeschlossener Kórper, l'Enseignement Mathématique (to appear).Google Scholar
[C-K] Chang, C.C. and Keisler, H.J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[E] Ershov, Yu. L., On the elementary theory of maximal normed fields, Doklady Akademie Nauk SSSR, vol. 165 (1965), Soviet Mathematics. Doklady, pp. 1390–1393.Google Scholar
[F] Fuchs, L., Partially ordered algebraic systems, Pergamon Press, Oxford, 1963.Google Scholar
[L-L] Läuchli, H. and Leonard, J., On the elementary theory of linear order, Fundamenta Mathematicae, vol. 59 (1966), pp. 109–116.CrossRefGoogle Scholar
[M] Macintyre, A., Classifying pairs of real closed fields, Ph. D. Dissertation, Stanford University, 1968.Google Scholar
[P] Prestel, A., Lectures on formally real fields, IMPA, Rio de Janeiro, 1975.Google Scholar
[R] Robinson, A., Solution of a problem of Tarski, Fundamenta Mathematicae, vol. 47 (1959), pp. 179–204.CrossRefGoogle Scholar